Linear_optimation

Linear and Network Optimization

一共有三章:

第一部分 Linear Problem 问题

Notation:

Standard form LP

\[\begin{align*} P &= \text{ feasible space} \\ &= \{ x \in \mathbb{R}^{n} | A \boldsymbol{x} = \boldsymbol{b}, \boldsymbol{x}\ge0 \} \\ \end{align*}\]

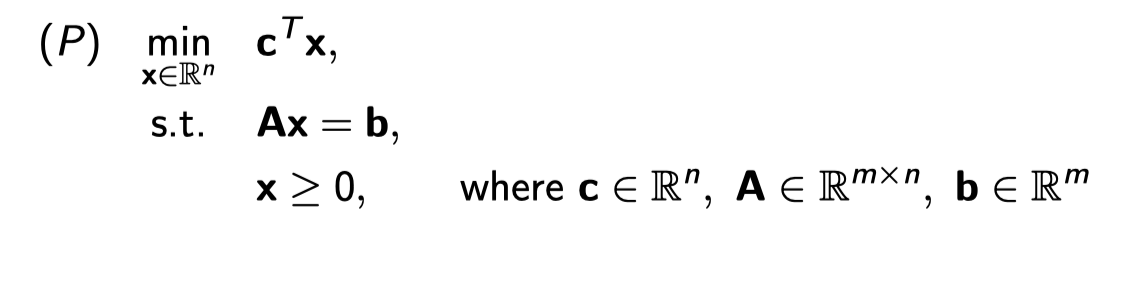
Basic feasible solution \(\boldsymbol{x}\)

\[\begin{align*} \boldsymbol{B} & = ( A_{B(1)} \; A_{B(2)} \; \cdots \; A_{B(m)} ) \\ B(m) & = \text{ 就是第几列的意思} \\ \boldsymbol{x}_B & = \left(\begin{array}{ccc} x_{B(1)} \\ \vdots \\ x_{B(2)} \\ \end{array} \right) \\ & = \boldsymbol{B}^{-1} \boldsymbol{b} \ge 0 \\ \end{align*}\]

Feasible direction

\[\begin{align*} d &= \text{ feasible direction } \\ & \text{ if } \boldsymbol{x} + \theta \boldsymbol{d} \in P \end{align*}\]

但我们其实更感兴趣的是, 沿着这个多边形, 这个d 怎么移动。这时候应该把它理解成：

增加一个单位的 X1 需要 X_B 怎样的变化？

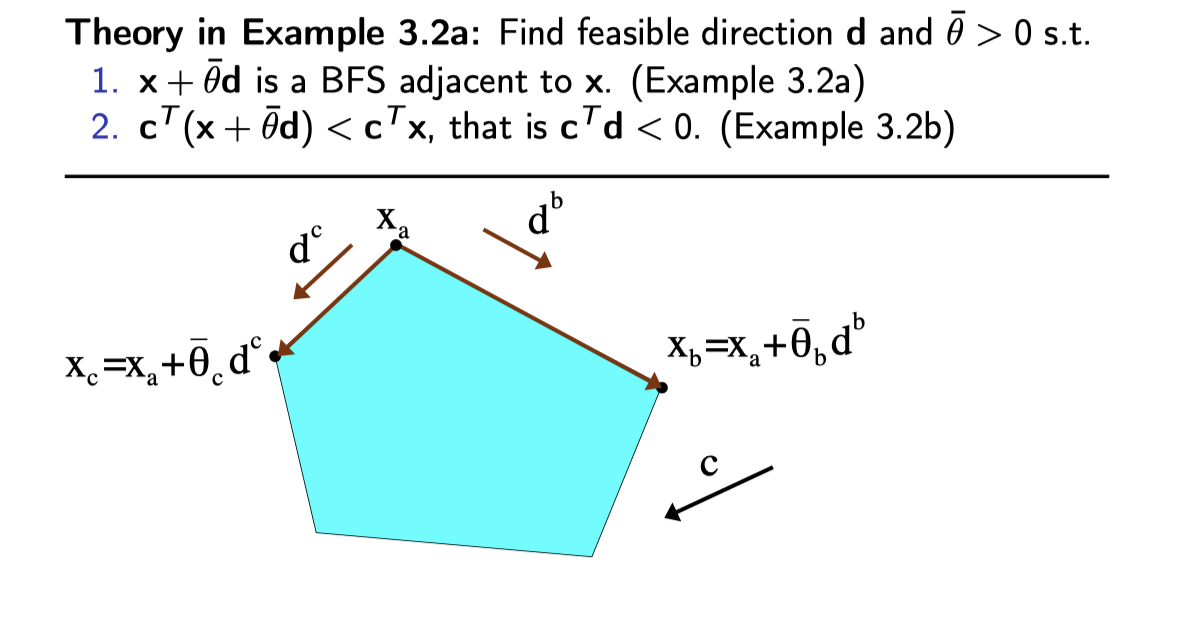
所以

\[\begin{align*} A_1 &= \text{ 增加一单位的 X_1 它的 对应的slack的变化}\\ A_1 + B d_B^1 &= 0 \\ d_B^1 &= -B^{-1} A_1 \\ &= \text{ d 只是代表一个比例 of } X_B \text{ , } \theta \text{ 代表的是 多少个单位的 } X_1 \end{align*}\]

所以 才有：

\[\begin{align*} \boldsymbol{x}_B + \bar{\theta} \boldsymbol{d} &= \boldsymbol{x}_{B2} \\ \end{align*}\]

对应的 reduced cost 就是 “ 1单位目标 j 的原本的 cost” - [去取代它的1单位其它填充部分的cost]

\[\boldsymbol{c}^T \boldsymbol{d}^j = ( \boldsymbol{c}_B, \boldsymbol{c}_N)^T \begin{align*} \left(\begin{array}{ccc} d_B^j \\ d_N^j \\ \end{array} \right) \end{align*} = \boldsymbol{c}_j - \boldsymbol{c}_B^T B^{-1} A_j.\\ \boldsymbol{c}_j = \boldsymbol{c}_N^T \boldsymbol{d}_N^j \\ \boldsymbol{d}_N^j\text{ 就是 只有 目标方向 j 是1 其它都是0}\\\]

Simplex Method

1. Start with B and BFS
2. Compute reduced cost (if all >=0 END with optimal, if some <0 then next) Selected a negative variable.

Auxiliary LP

This is a method to see the constraints are feasible or not.

example

Standard LP:

\[\begin{align*} & \min &4x_1 &+ &x_2 & & & & &\\ & s.t. &3x_1 &+ &x_2 & & & &= &3 \\ & &4x_1 &+ &3x_2 & & &-s_1 &= &6\\ & &x_1 &+ &2x_2 & & &+s_2 &= &4\\ & & & & & & &x_1,x_2,s_1,s_2 & \ge &0\\ \end{align*}\]

Then only focus on those non positive slack:

然后我们去找这个新 Auxiliary LP 的 optimal, 如果是

sum of y	means
0	feasible
>0	infeasible
<0	not possible since y >0

一样的也是 simplex tableau, 但要先构造 reduced cost

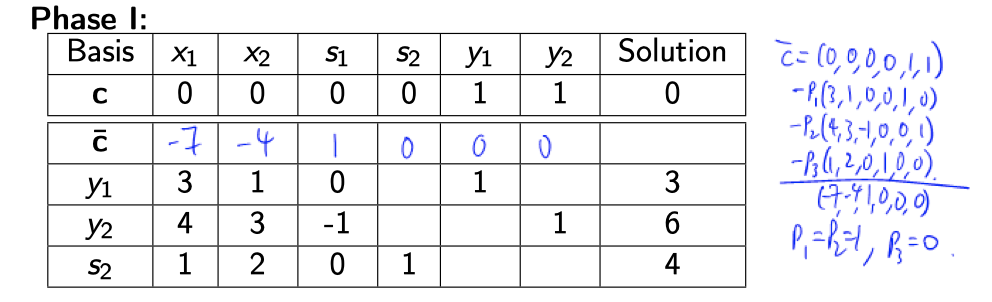
为什么是这样构造呢？

Two-Phase Method

Phase I: Find BFS using auxiliary LP (to see if it is feasible or not)

if not feasible (end),

if feasible: Phase II: Simplex method to get the optimum or detects unboundedness.

Dual LP

Example

我们先来看一个 最最 trivial 的example：

Primal \(\begin{align*} \max 4&x \\ x &\le 5 \\ x &\ge 0 \\ \end{align*}\)

Dual \(\begin{align*} \min 5&y \\ y &\ge 4 \\ y &\ge 0 \\ \end{align*}\)

如果把 primal 当作是 拥有5个产品, 每个售价是4块。最大利润是多少. (我们只能控制卖多少产品)

如果把 dual 的 y 当作是 售价, 我们要把5 个产品全卖掉, 但是我们售价”至少”是4块, 我们想看, 如果我们只能控制价格, 我们至少要赚多少钱。 最少买多少钱。

[重要总结] 其实这两个问题就是不一样的问题, 我在学的时候, 老是觉得很疑惑, 这两个 P & LP 到底是怎么理解, 它们为什么是 equivalent 的。 其实不是的, 它们压根就不是 equivalent 的问题, 只是 “恰好” 它们的 optimal 是相等的！

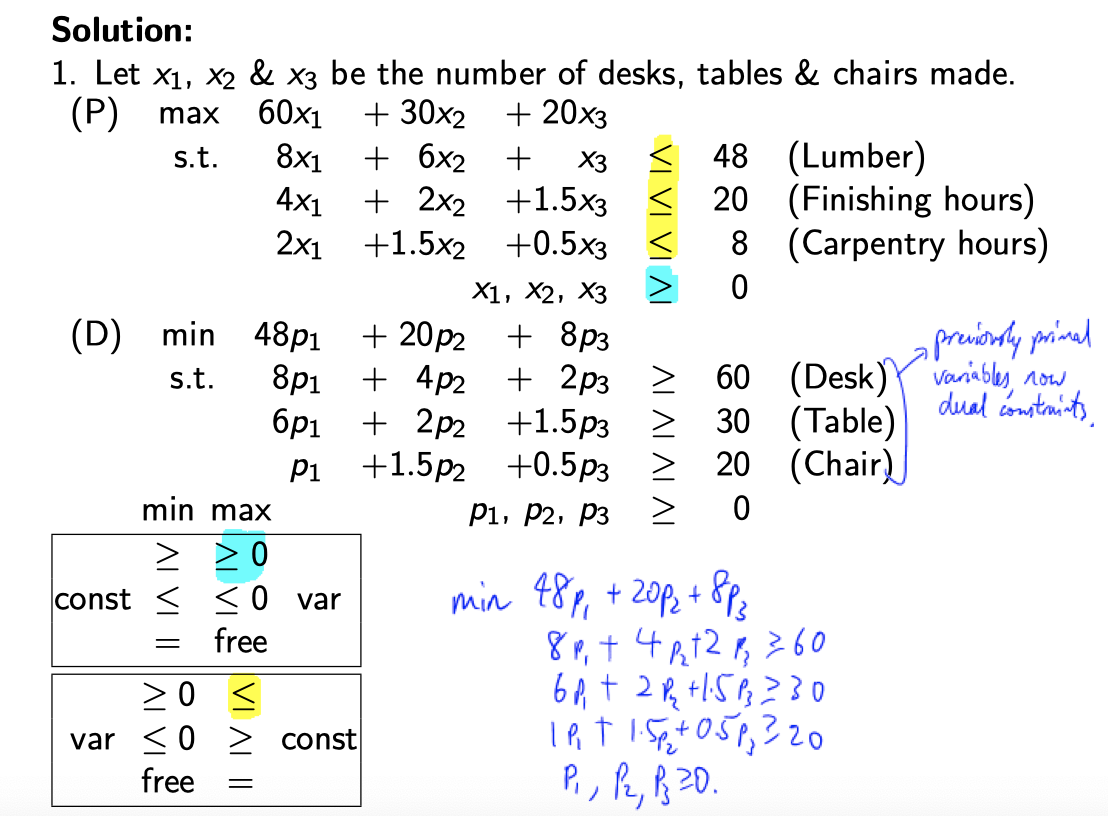
注意： 中间的Matrix \(A_{}^{}\) 是 \(A_{}^{T}\) 了

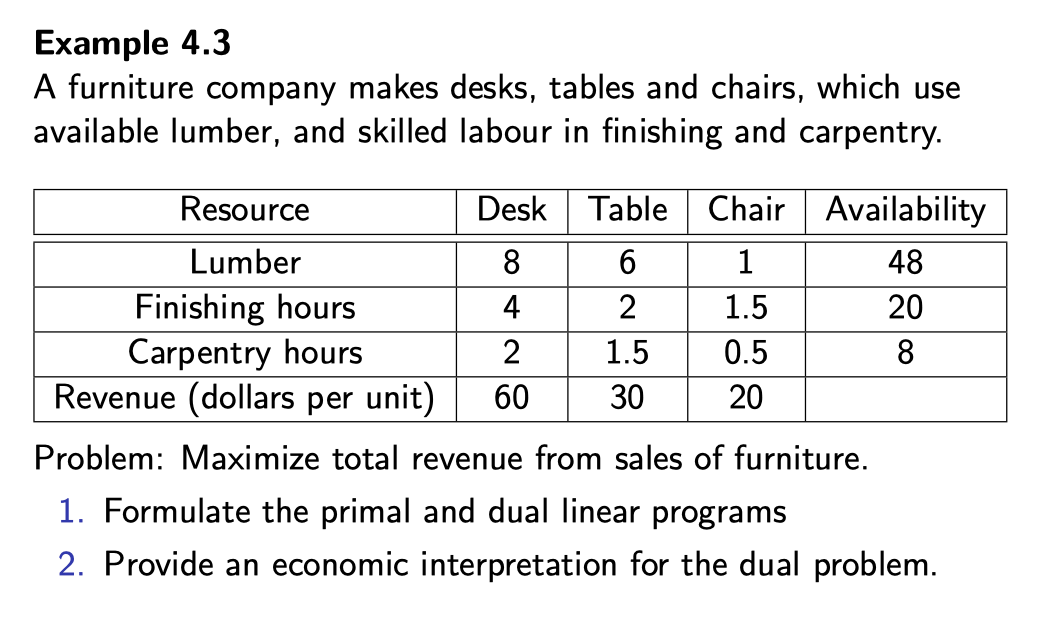
[这是我一开始学的问题] 简单的理解就是, 把b 和 c 对换, 但是为什么 Lumber 对应 Desk ？？ Finishing 对应 Table ？？ 这两个根本说不通呀。而且这是, 3 对 3 的例子, 完全可以 4 对 2, 不一定是一一对应的呀。

Primal 问题是, 已有这些resource, 怎样maximize 利润。x 是指多少单位的 桌子凳子。

Dual 问题是, 已有最低的成本价, 我们怎么把平均的成本降到最低。？？？

[现在我懂了] 我们相等于把, 桌子椅子的按它的原料卖, 就是一个桌子是由 8 单位木材, 4 小时的 finishing hour 和 2 小时的carpentry hours, 造成的, 其它的类似, 现在, 我把全部的 已有的原料 全部压缩打成粉末再全部组装卖给你, (所有的资源都用上了), 现在我可以任意制定价格, 但是呢, 现在的问题是, 我要让我的价格 (至少比我之前定的价格高！)。看到了吗！ 这就是为什么！！它们的optimal 恰好相等！ 因为它就是这样设计的！

[下面有误, 我乱写的, 以后再修改] 所以一样的, 为什么 Integral problem的时候, 它的duel 给了一个lower bound, 它就是相等于是一个 relaxed

Upper bound is easy to find (any feasible \(x’\) corresponding \(c^T x\))

Lower bound

Define:

\( \displaystyle g(p):= \min_{x\in \mathbb{R}^{n}} c^T x + p^T (b-Ax) \)

Lower bound can be construct in this form: \( \displaystyle g(p) \le c^T x^* + p^T (b-Ax^* ) \) where \((b-Ax^* )\) should be \(0\) and \(x^*\) is an optimal solution.

所以,

\[\begin{align*} g( \boldsymbol{p}) = \boldsymbol{p}^T \boldsymbol{b} + \min_{x\ge 0} (\boldsymbol{c}^T - \boldsymbol{p}^T \boldsymbol{A}) \boldsymbol{x} = \boldsymbol{p}^T \boldsymbol{b} &+ \begin{cases} 0 & \text{ if } \boldsymbol{c}^T - \boldsymbol{p}^T \boldsymbol{A} \ge 0 \\ - \infty & \text{otherwise} \end{cases} \\ \end{align*}\]

Sensitivity Analysis 敏感度分析

就是分析现有的LP，改变一点点条件会如何影响Solution; ( \(b\), \(c\), \(A\), \(x\) (new variable), new constraints)

Change \(b\)

Dual Simplex Method

第二部分： Network Optimisation 网络

Flow balance constraint

Flow out - Flow in = Supply

Notation: \(\begin{align*} x_{ij} &= \text{The amount of flow through arc } (i,j) \in E \\ b_i &= \text{External supply/demand for node } i \\ b_i &< 0 \text{ demand node.}\\ b_i &> 0 \text{ supply node.}\\ b_i &= 0 \text{ transshipment node.}\\ u_{ij} &= \text{The upper bound.}\\ c_{ij} &= \text{ the post per unit flow on the arc.} \end{align*}\)

Definition

• Graph
• Cycle
• acyclic No cycle
• Tree a connected acyclic graph
• Bipartite If nodes can be divided into two sets such that the end nodes for each edge lie in different sets.
• Node-arc incidence matrix

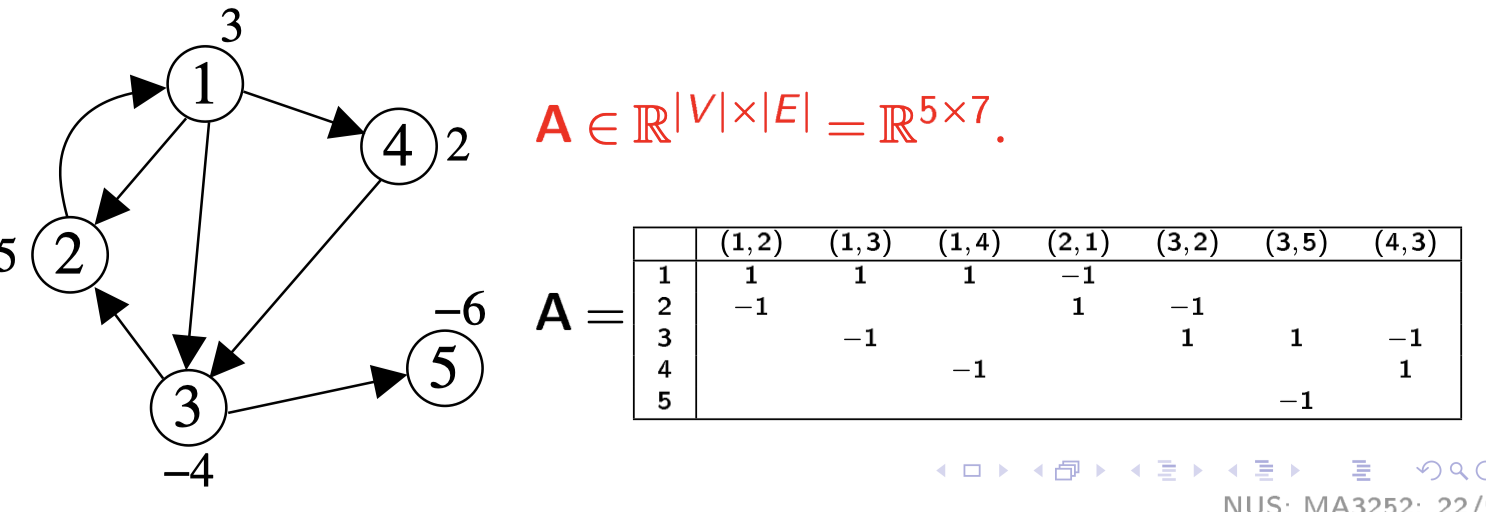
Network Flow Formulation

Types of network flow problems:

• Shortest Path problem: minimum time/length
• Maximum flow problem: Maximum steady state flow
• Minimum cost flow problem

Minimum cost flow problem

Standard form of a network flow problem:

\[\begin{align*} &min & & c^Tx &\, \\ &s.t & & Ax = b \\ &\, & & 0 \le x \le u &\, \\ \end{align*}\]

Shortest Path problem: minimum time/length 最短路径问题

Make the node \(b_{ij} = 0\) except the one at the start point and the end point.

\(b_{start} = 1 \);
\(b_{end} = -1\)

And also \(x_{i,j} \in { 0,1 } \), \(x\) variable only determine which road should be picked.

Now: if we relax the binary constrain: From (P1) \(\to\) (P2).

We have:

Theorem

If there are no negative cycles, then (P2) is also the shortest path problem. (The proof is omitted (will be studied in MA4254 (Discrete Optimization[Dijkstra’s algorithm; and Bellman-Ford and Floyd-Warshall algorithms for negative cycles]))).

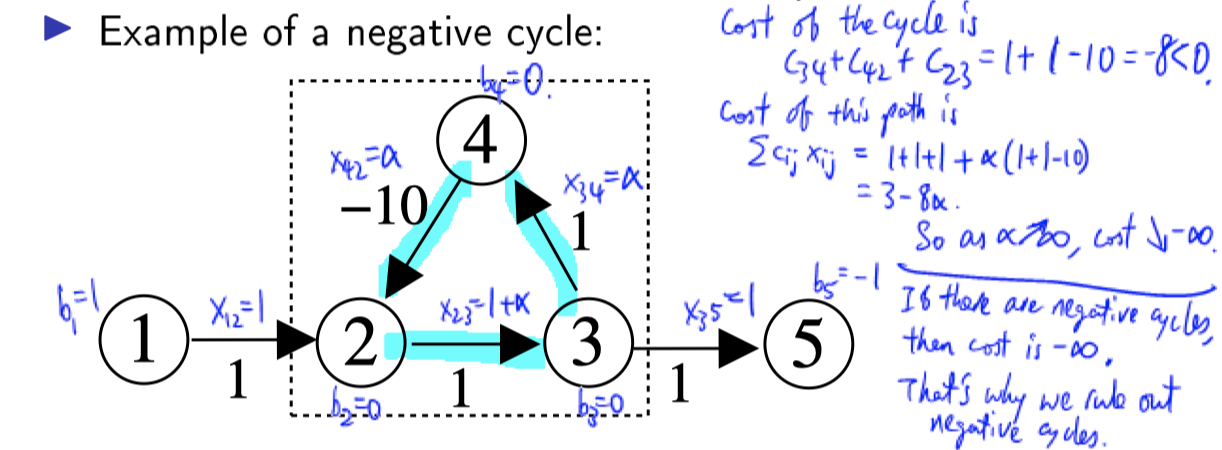
Negative Cycle:

Three Jug Puzzle Application

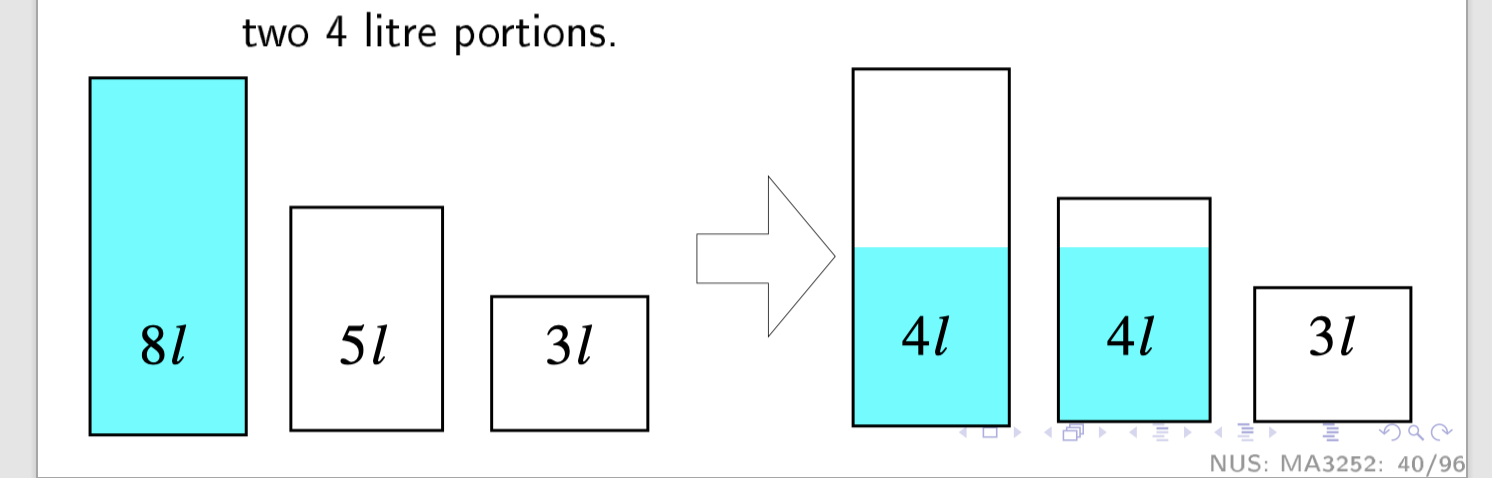
这个也是挺妙的运用。 如何把这个问题转成 最短路径问题: 核心是用坐标表示瓶子的状态： e.g. (5，3) 五升的瓶子有5L水，三升的瓶子有3L水。 然后我们就可以define path 不同瓶子里水倒来倒去。

Dynamic Lot Sizing Application

Question Notation:
\(T\) time periods \( { 1,2,…,T } \)
\(d_i\) Demand of period \(i\).
\(x_i\) Produce in period \(i\)
\(I_{i-1}\) Inventory level.
\(c_i\) cost of producing one unit product

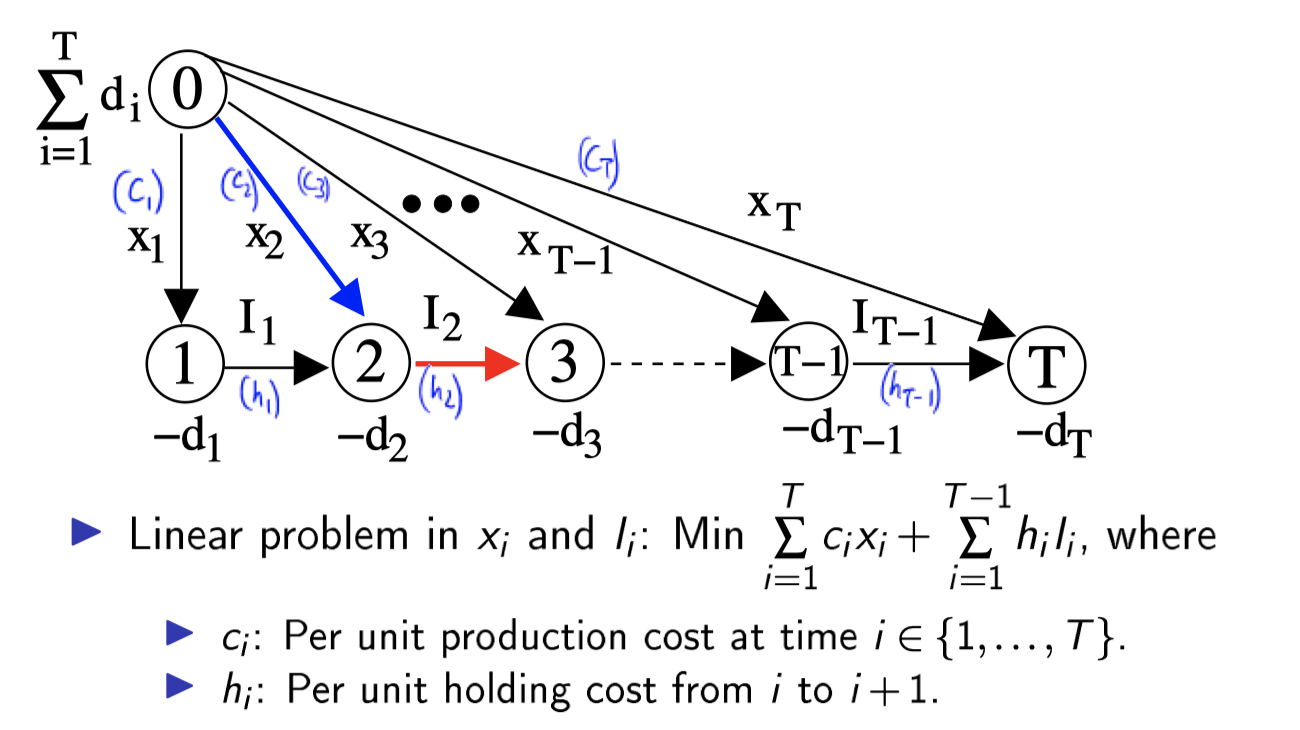
可以把这个问题拆成 \(T\) 个shortest path problem:
就是可以把每个 \(d_i\) 作为一个小终点，然后把所有的solution 加在一起那就是最后的答案了。

• Key Production Property: 最后的solution会
  1. Not both carry inventory and produce: 一个node的需求 不会要同时 “生产” & “库存”来满足。[除非上一个库存不要钱(或者甚至是负的)] [而且 setup cost 不为0]
  2. Each \( \displaystyle x_i = \sum_{k\le i}^{} d_k \) 其实这个也是同理于第一点。

例题：

待补充。

Duality in shortest path problem

Example:

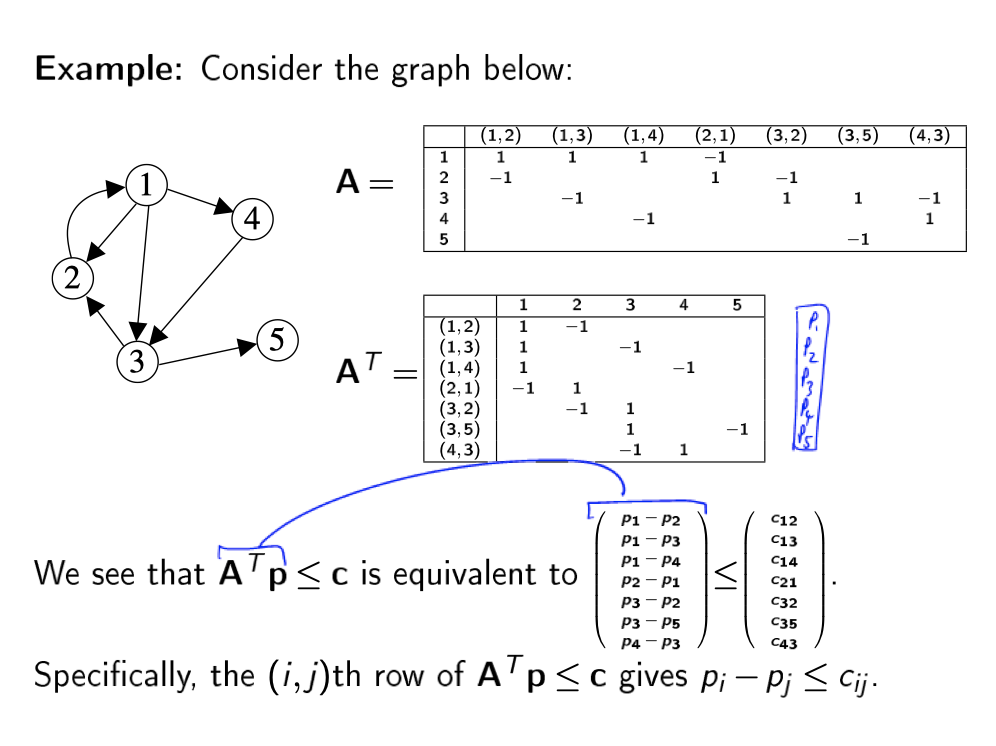
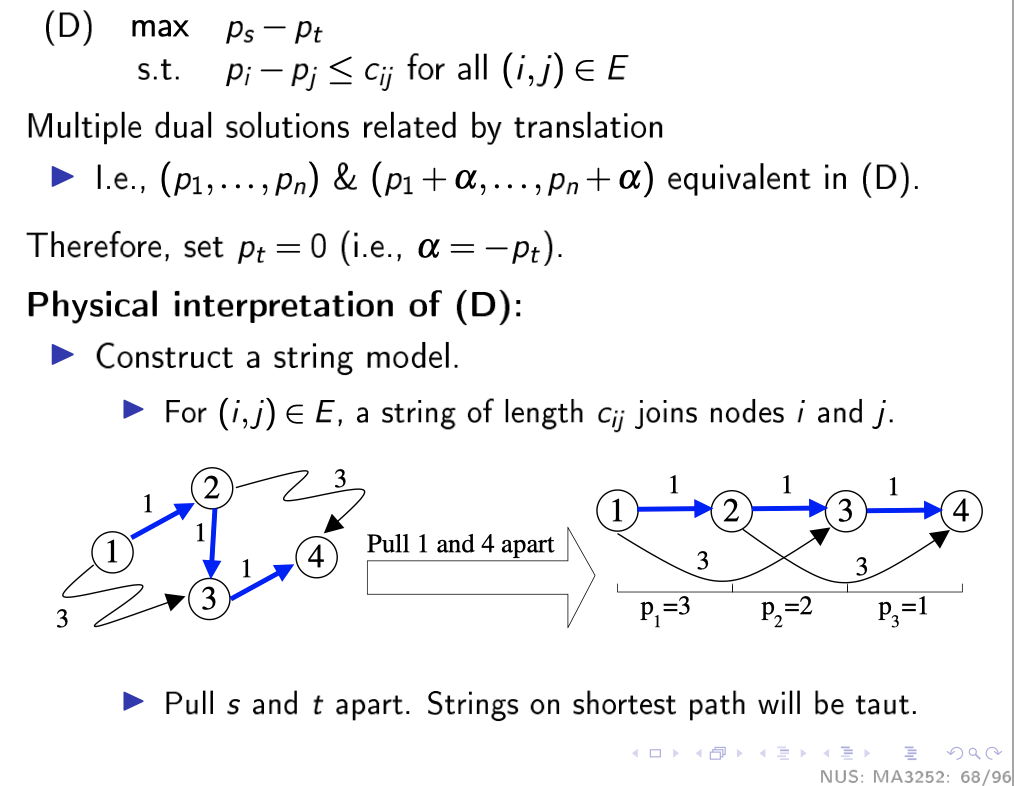
Intuitive understanding of the Dual problem:

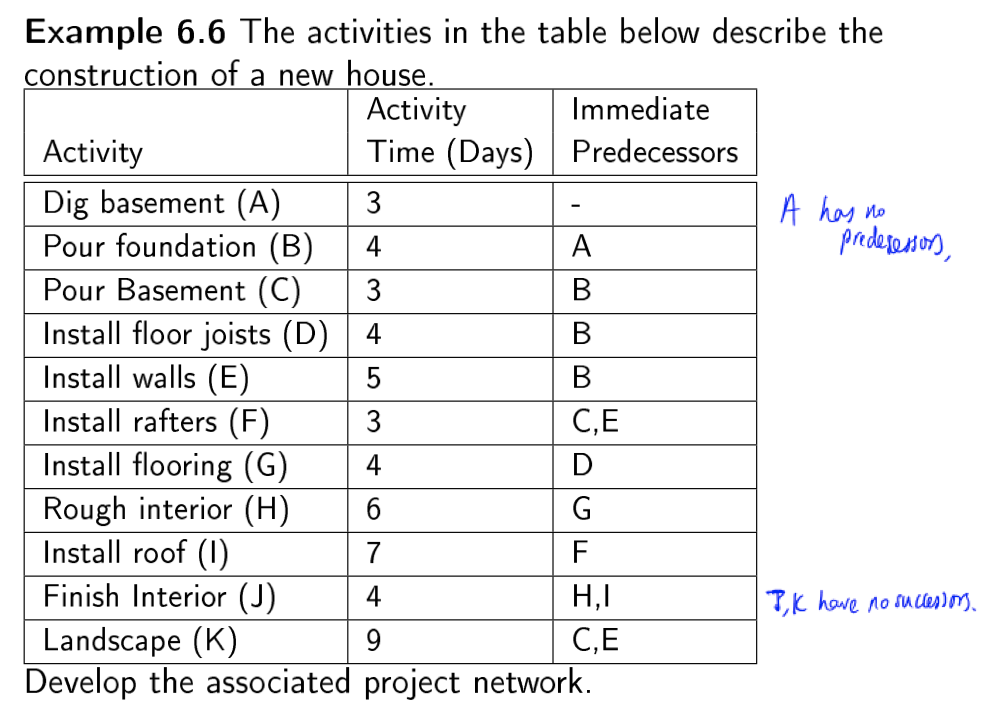
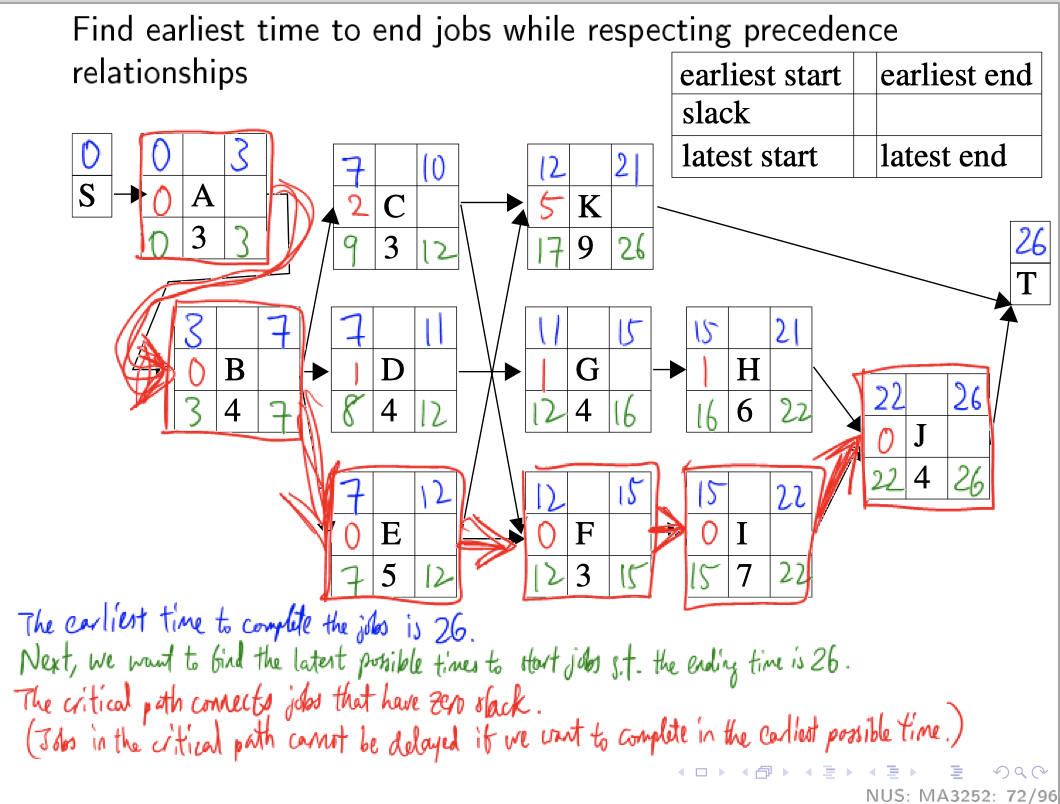
Project Management Application

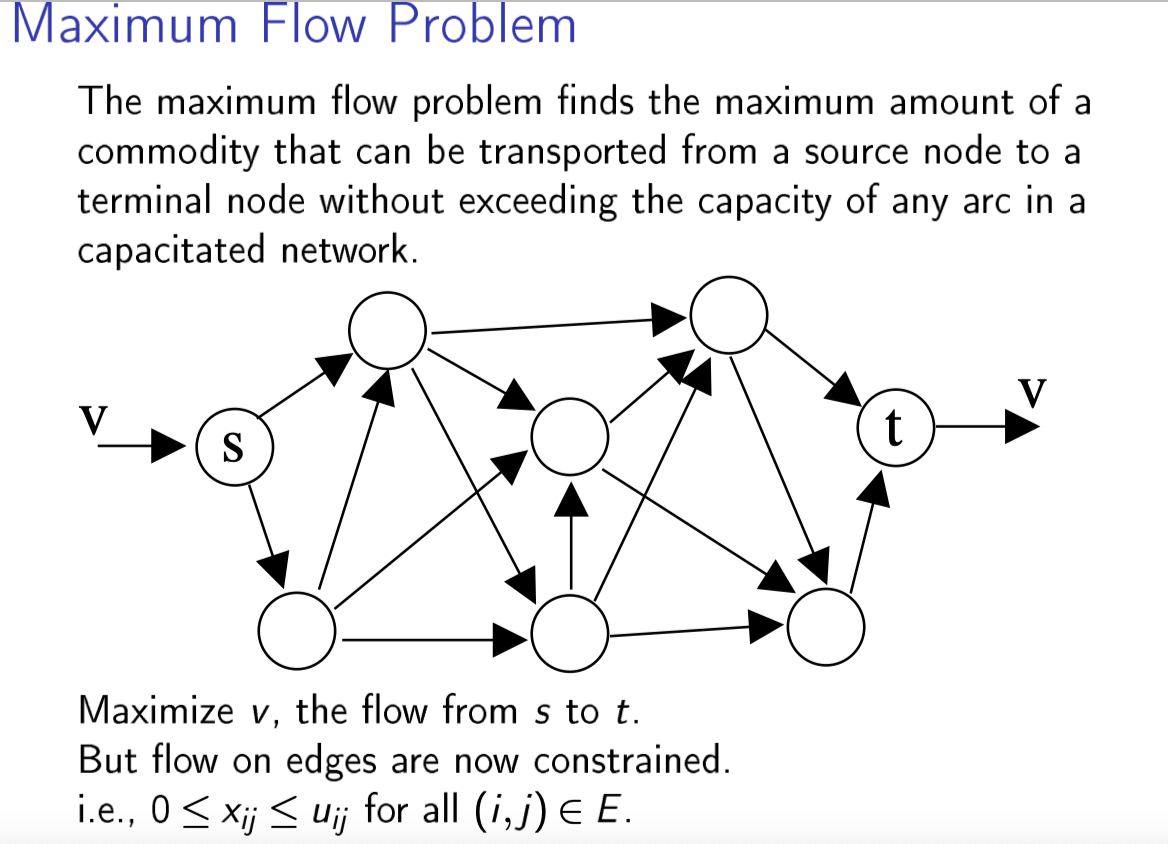
Maximum Flow Problem

Duality in maximum flow problem

Cut

A Cut is a partition of V into two subsets \( \bar{S} = V\setminus S\)

• Forward arcs: from nodes in \(S\) to nodes in \(\bar{S}\). denote \((S,\bar{S})\)
• Backward arcs: from nodes in \(\bar{S}\) to nodes in \(S\). denote \((\bar{S},S)\)
• s-t cut, \( s \in S, t \in \bar{S}\)
• capacity of a cut: the sum of the capacities of the forward arcs. \( \displaystyle u(S, \bar{S}) = \sum_{(i,j) \in (S, \bar{S})}^{} u_{i,j}\)

Simplex 算法

Duality 对偶性

Primal

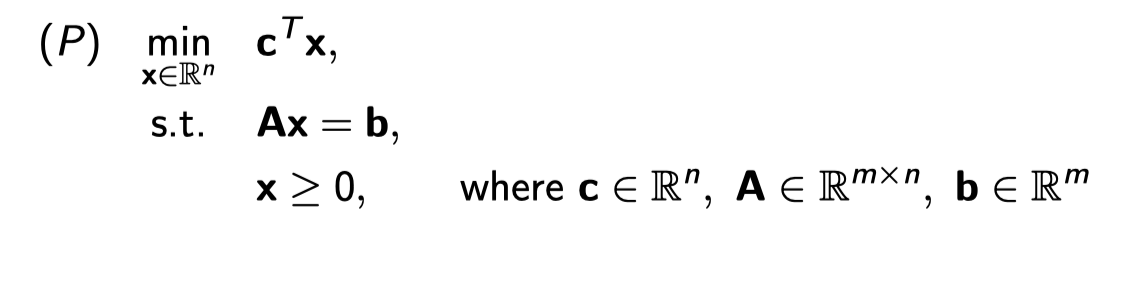
Upper bound is easy to find (any feasible \(x’\) corresponding \(c^T x\))

Lower bound

Define:

\( \displaystyle g(p):= \min_{x\in \mathbb{R}^{n}} c^T x + p^T (b-Ax) \)

Lower bound can be construct in this form: \( \displaystyle g(p) \le c^T x^* + p^T (b-Ax^* ) \) where \((b-Ax^* )\) should be \(0\) and \(x^*\) is an optimal solution.

所以,

\[\begin{align*} g( \boldsymbol{p}) = \boldsymbol{p}^T \boldsymbol{b} + \min_{x\ge 0} (\boldsymbol{c}^T - \boldsymbol{p}^T \boldsymbol{A}) \boldsymbol{x} = \boldsymbol{p}^T \boldsymbol{b} &+ \begin{cases} 0 & \text{ if } \boldsymbol{c}^T - \boldsymbol{p}^T \boldsymbol{A} \ge 0 \\ - \infty & \text{otherwise} \end{cases} \\ \end{align*}\]

Sensitivity Analysis 敏感度分析

就是分析现有的LP，改变一点点条件会如何影响Solution; ( \(b\), \(c\), \(A\), \(x\) (new variable), new constraints)

Change \(b\)

第二部分： Network Optimisation 网络

Flow balance constraint

Flow out - Flow in = Supply

Notation: \(\begin{align*} x_{ij} &= \text{The amount of flow through arc } (i,j) \in E \\ b_i &= \text{External supply/demand for node } i \\ b_i &< 0 \text{ demand node.}\\ b_i &> 0 \text{ supply node.}\\ b_i &= 0 \text{ transshipment node.}\\ u_{ij} &= \text{The upper bound.}\\ c_{ij} &= \text{ the post per unit flow on the arc.} \end{align*}\)

Definition

• Graph
• Cycle
• acyclic No cycle
• Tree a connected acyclic graph
• Bipartite If nodes can be divided into two sets such that the end nodes for each edge lie in different sets.
• Node-arc incidence matrix

Network Flow Formulation

Types of network flow problems:

• Shortest Path problem: minimum time/length
• Maximum flow problem: Maximum steady state flow
• Minimum cost flow problem

Minimum cost flow problem

Standard form of a network flow problem:

\[\begin{align*} &min & & c^Tx &\, \\ &s.t & & Ax = b \\ &\, & & 0 \le x \le u &\, \\ \end{align*}\]

Shortest Path problem: minimum time/length 最短路径问题

Make the node \(b_{ij} = 0\) except the one at the start point and the end point.

\(b_{start} = 1 \);
\(b_{end} = -1\)

And also \(x_{i,j} \in { 0,1 } \), \(x\) variable only determine which road should be picked.

Now: if we relax the binary constrain: From (P1) \(\to\) (P2).

We have:

Theorem

If there are no negative cycles, then (P2) is also the shortest path problem. (The proof is omitted (will be studied in MA4254 (Discrete Optimization[Dijkstra’s algorithm; and Bellman-Ford and Floyd-Warshall algorithms for negative cycles]))).

Negative Cycle:

Three Jug Puzzle Application

这个也是挺妙的运用。 如何把这个问题转成 最短路径问题: 核心是用坐标表示瓶子的状态： e.g. (5，3) 五升的瓶子有5L水，三升的瓶子有3L水。 然后我们就可以define path 不同瓶子里水倒来倒去。

Dynamic Lot Sizing Application

Question Notation:
\(T\) time periods \( { 1,2,…,T } \)
\(d_i\) Demand of period \(i\).
\(x_i\) Produce in period \(i\)
\(I_{i-1}\) Inventory level.
\(c_i\) cost of producing one unit product

可以把这个问题拆成 \(T\) 个shortest path problem:
就是可以把每个 \(d_i\) 作为一个小终点，然后把所有的solution 加在一起那就是最后的答案了。

• Key Production Property: 最后的solution会
  1. Not both carry inventory and produce: 一个node的需求 不会要同时 “生产” & “库存”来满足。[除非上一个库存不要钱(或者甚至是负的)] [而且 setup cost 不为0]
  2. Each \( \displaystyle x_i = \sum_{k\le i}^{} d_k \) 其实这个也是同理于第一点。

例题：

待补充。

Duality in shortest path problem

Example:

Intuitive understanding of the Dual problem:

Project Management Application

Maximum Flow Problem

Duality in maximum flow problem

Cut

A Cut is a partition of V into two subsets \( \bar{S} = V\setminus S\)

• Forward arcs: from nodes in \(S\) to nodes in \(\bar{S}\). denote \((S,\bar{S})\)
• Backward arcs: from nodes in \(\bar{S}\) to nodes in \(S\). denote \((\bar{S},S)\)
• s-t cut, \( s \in S, t \in \bar{S}\)
• capacity of a cut: the sum of the capacities of the forward arcs. \( \displaystyle u(S, \bar{S}) = \sum_{(i,j) \in (S, \bar{S})}^{} u_{i,j}\)