Stochastic_operation_research_note

Stochastic Operation Research note

一共有三章:

1. Queueing Theory

2. [Inventory Theory](#ch2 “”)

   2.1. Deterministic(#ch2.1 “”)

   2.2. [Probabilistic](#ch2.2 “”)

3. Stochastic Programming

Theory

2.1. [Deterministic](#ch2.1 “”)

2.2. [Probabilistic](#ch2.2 “”)

1. Stochastic Programming

2. Inventory Theory 库存管理

其实这也是非常intuitive的一章。

Notation: \(\begin{aligned} q &= \text{number of units ordered (decision variable).}\\ K &= \text{set up cost per ordre} \\ C &= \text{Purchase cost per item}\\ h &= \text{holding cost per item per unit time}\\ p &= \text{shortage penalty cost per item per unit time}\\ a &= \text{demand rate}\\ D &= \text{random variable (demand)}\\ Pr(D = d) &= p(d) \text{ probability realisation} \\ c(d,q) &= \text{cost function}\\ \end{aligned}\)

2.1. Deterministic Inventory Model

最简单的情况：

\[\begin{align*} {\frac{q}{a}} &= \text{Time length of one cycle.} \\ {\frac{q}{2}} &= \text{average inventory level}\\ h({\frac{q}{2}})&= \text{holding cost}\\ aC &= \text{purchase cost per unit time.}\\ K \div {\frac{q}{a}} &= \text{set up cost per unit time.}\\ TC(q) &= {\frac{aK}{q}} + aC + {\frac{hq}{2}} \\ q^* &= \sqrt{ {\frac{2aK}{h}} } \\ {\frac{q^*}{a}} &= \sqrt{ {\frac{2K}{ah}} } \text{ optimal cycle length}\\ \end{align*}\]

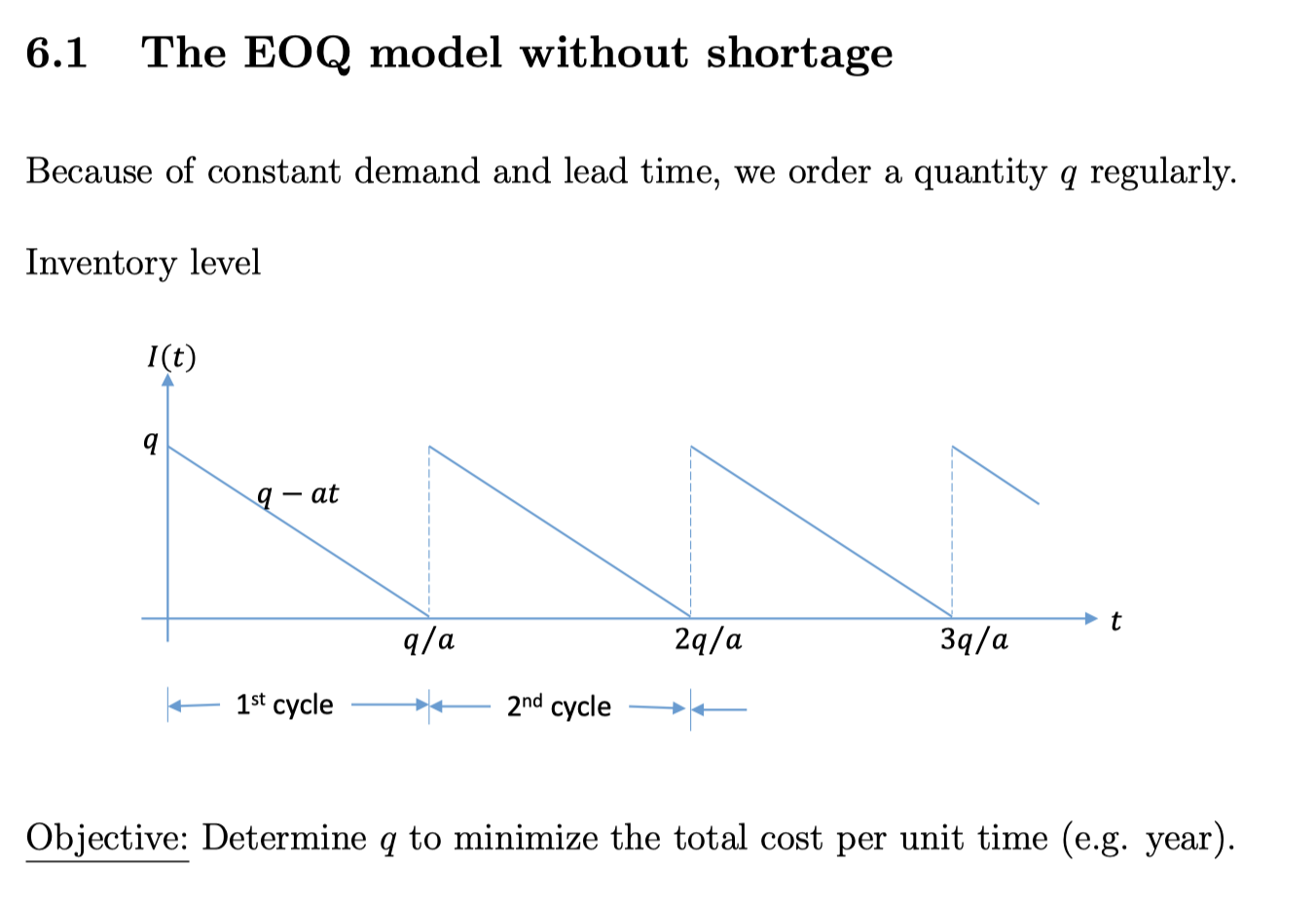
允许Shortage：

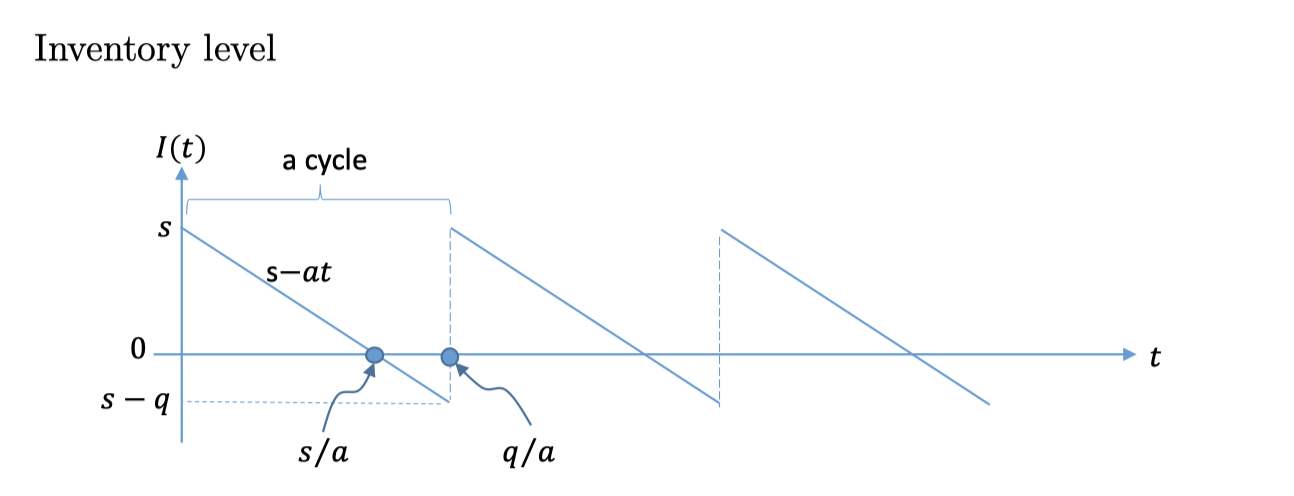
相当于多了一个option，允许shortage了，所以我们需要一个新的变量决定shortage 多久， \(S_{}^{}\)

\[\begin{align*} S &= \text{ the stock at the beginning of a cycle} \\ q &\ge S \\ {\frac{S}{a}} &= \text{ time length of without shortage}\\ {\frac{q}{a}} &= \text{ time length of a cycle} \\ {\frac{hS}{2}} {\frac{S}{a}} &= \text{ holding cost per cycle}\\ {\frac{hS}{2}} {\frac{S}{a}} \div {\frac{q}{a}} &= \text{ holding cost per unit time}\\ p &= \text{ shortage cost per item per unit time} \\ p( {\frac{q-S}{2}}) ( {\frac{q-S}{a}} ) &= \text{ shortage cost per cycle} \\ aC &= \text{ purchasing cost per unit time} \\ TC(q,S) &= {\frac{aK}{q}} + aC + {\frac{hS^2}{2q}} + {\frac{p(q-S)^2}{2q}} \\ \end{align*}\]

Then we can solve: \(\begin{align*} q^* &= \sqrt{ {\frac{2aK}{h}} } \sqrt{ {\frac{p+h}{p}} } \\ S^* &= \sqrt{ {\frac{2aK}{h}} } \sqrt{ {\frac{p}{p+h}} } \\ t^* &= {\frac{q^*}{a}} = \sqrt{ {\frac{2K}{ah}}} \sqrt{ {\frac{p+h}{p}} }\\ \lim_{p \to \infty} q^* &= \text{ in the previous casa, with shortage cost is infinity}\\ \end{align*}\)

EOQ with nonzero lead time

so 我们额外要解决的问题是, \(R_{}^{}\) reorder point 在哪里

\[R = \text{ reorder point} L = \text{ lead time }\\ \alpha L = \text{ demand occurred during lead time}\]

因为是 deterministic, 所以其实不怎么影响, 之前提前规划就可以了。所以 \(q_{*}^{}\) 都和之前一样。

Case 1, \(\underline{ a L \le q^*}\)

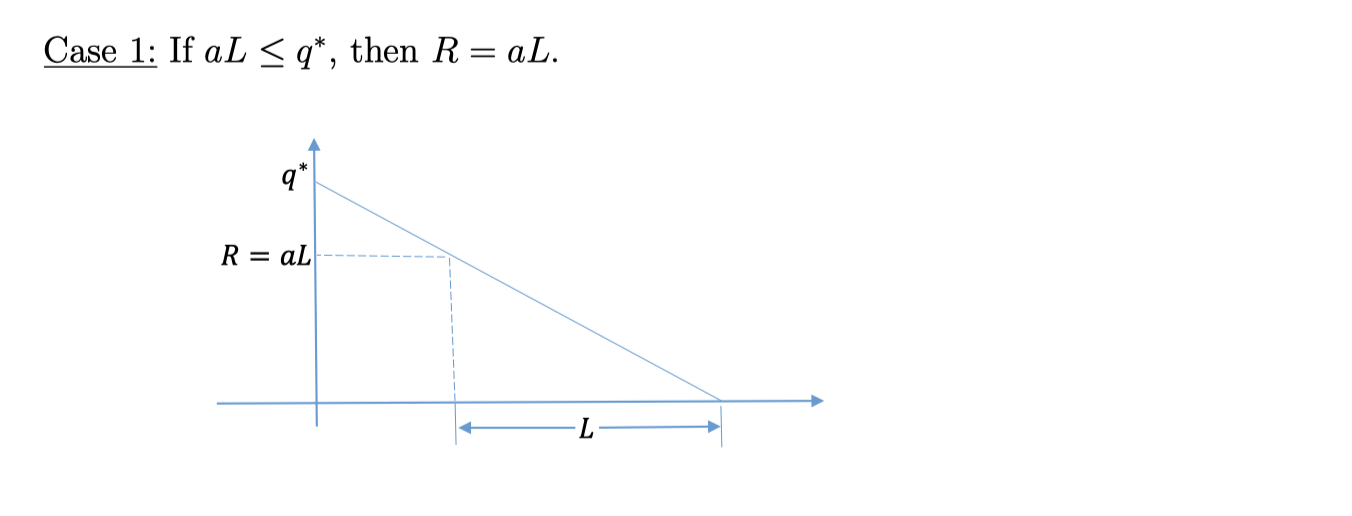
Case 2, \(\underline{ a L > q^* }\)

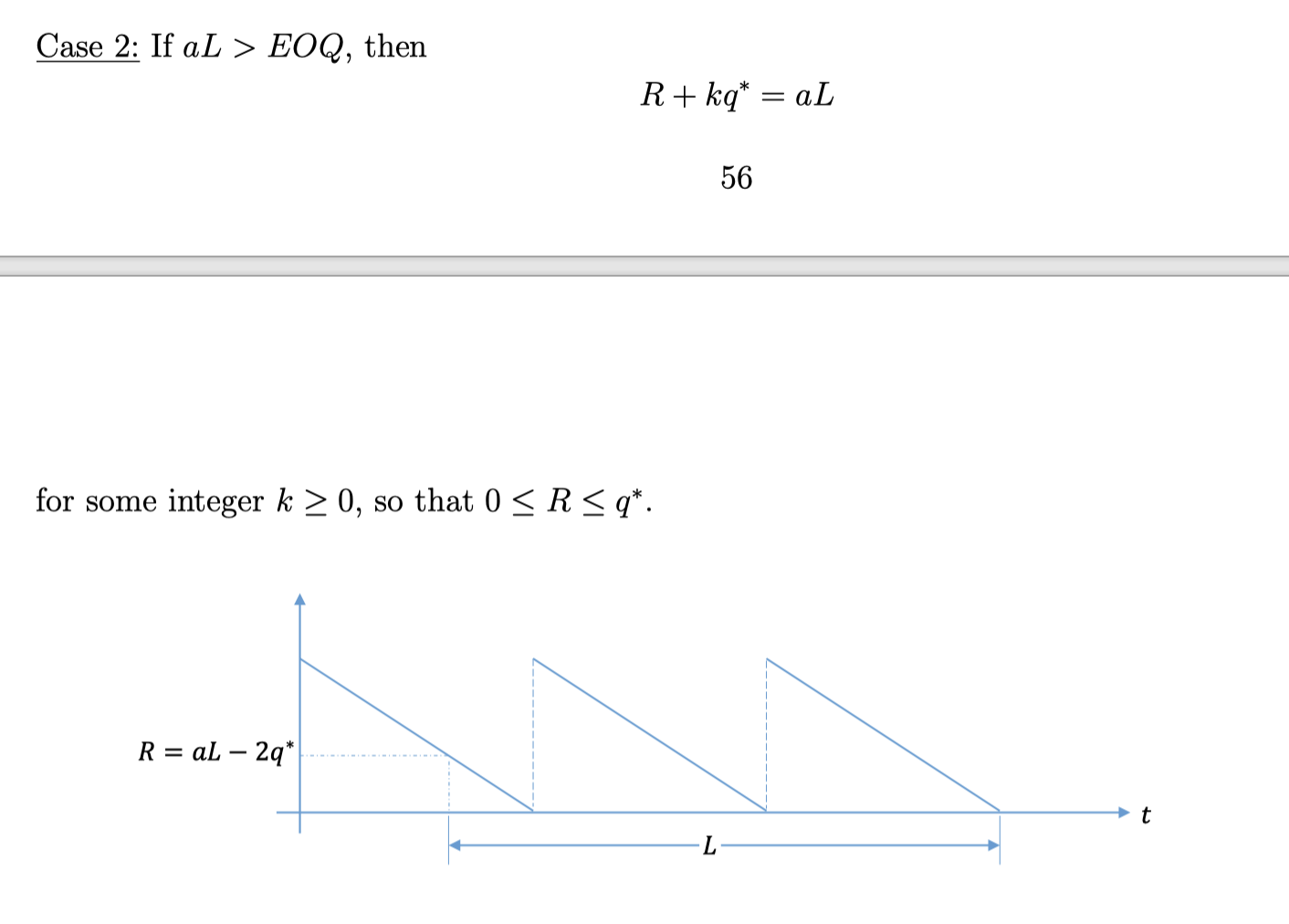
就是 一个 L 长于一个周期了已经, 所以要提前 2个周期以上订货。

Example

如果 \(q^* = 25298 \,\, a = 8000\)

如果 L = 2 month, aL = 16000 < 25298 Re-order point 就是 16000, 库存还剩 16000 的时候就要进货 \(q^*\) 的量

如果 L = 9 month, aL = 72000 > 25298 Re-order point 就是 \(aL - k*q^*\) 找到一个 k, 让它恰好 在 \(< q^*\) 的区间内, 这个例子是 k = 2 , 既 库存还剩 72000 - 2 * 25298 的时候就要进货 \(q^*\) 的量

Continuous - rate EOQ model

这次, 货物不是凭空长的, 是一点一点运进去的, 所以有了 这个continuous model

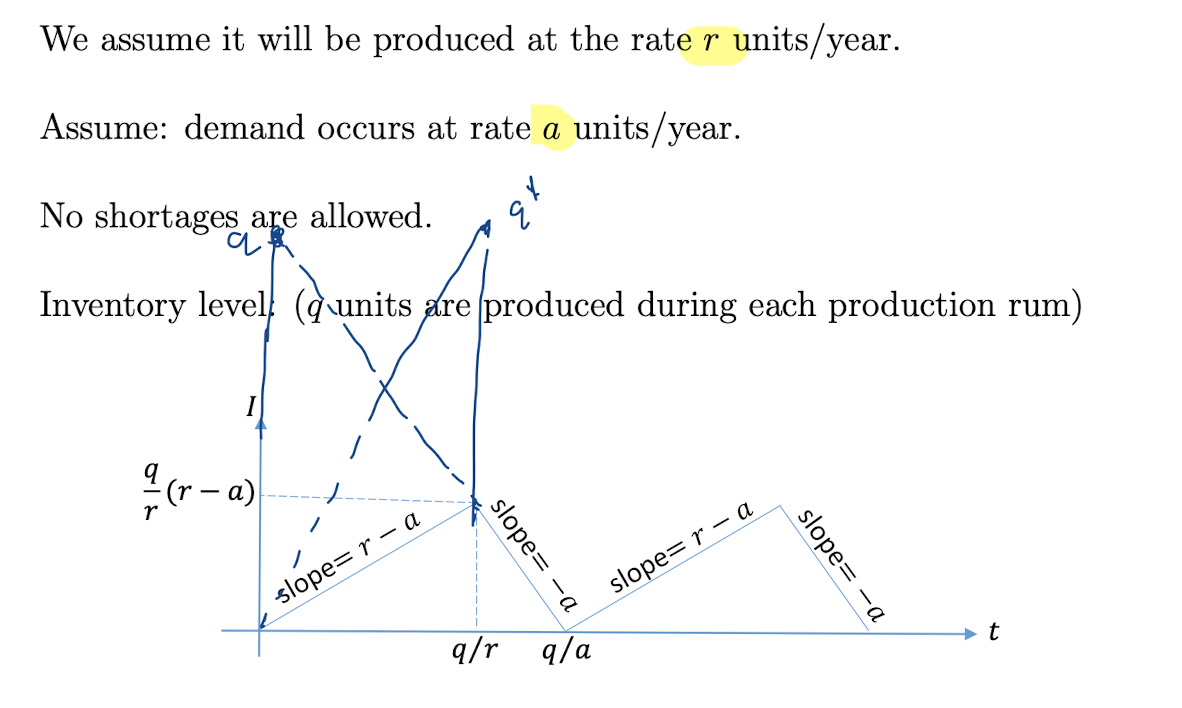
Notation:

\[\begin{align*} r &= \text{ 进货的速度} \\ a &= \text{ 需求速度} \\ {\frac{a}{q}} &= 一年有这么多个 cycle \\ {\frac{q}{a}} &= 一个cycle (unit time) 占多少年 \\ \end{align*}\]

从图像三角形的面积得出： \(\begin{align*} \text{holding cost per cycle }&= {\frac{1}{2}} {\frac{q}{r}} (r - a) \cdot {\frac{q}{a}} \cot h = {\frac{h q^2 (r-a) }{2ra}} \\ \text{ total cost per unit time}TC(q) &= {\frac{Ka}{q}} + Ca + {\frac{hq(r-q)}{2r}}\\ \end{align*}\)

结论： \(\begin{align*} q^* &= \sqrt{ {\frac{2Kar}{h(r-a)}} } \\ \end{align*}\)

买多有打折问题

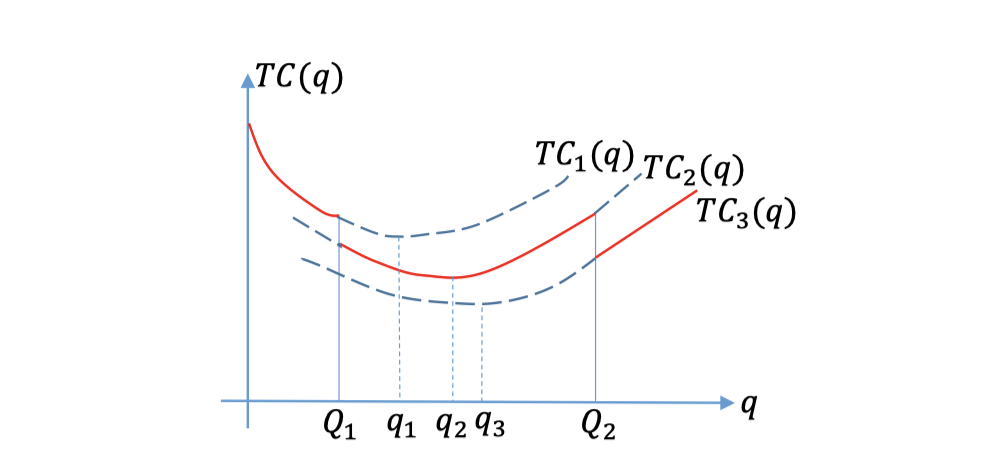
买的越多越便宜, 所以很明显的, 最低点就在每一段的 \(q^*\) 点, 或者在下一段的开头点.

Periodic review Model ( 最短距离问题)

前提假设

1. Demand 不连续
2. 进货 L = 0
3. No shortages

Notation：

\[\begin{align*} i (i = 1,2,3...,N) &= \text{period} \\ r_i &= \text{demand for peroid i }\\ K_i &= \text{set up cost if purchases in i}\\ c_i &= \text{ i 时段的单价} \\ h_i &= \text{ i 时段的储藏费} \\ & \\ x_i &= \text{ i 时刻的库存量, 被消费前}\\ z_i &= \text{ i 时段的购买量}\\ x_{i+q} &= x_i + z_i - r_i \text{ 下一时段的库存量 = 上一次的库存 + 买的 - 被消费的}\\ \end{align*}\]

Example

首先,

把整个路径的都画出来。

然后 从后往前的遍历全部路径

然后找到最优的方案。

2.2. Probabilistic Inventory Model

• 2.2.1 Optimal Cost
  1. Without Lead time
  2. With Lead time
  3. Allowed Shortage (Back logged case)
  4. Lost Sales Case 顾客直接不买了
  5. (s,S) policies 如果demand 不连续，一次可能被买穿
• 2.2.2 Service Level 考虑 百分之多少的时间会被买穿
• 2.2.3 Periodic Review Models (R,S) Policies 固定时期要检查一次库存

Without Lead time: Marginal Analysis (\(\frac{\alpha}{\beta}\) Method)

\[\begin{align*} C_u(d,q) &= - \alpha q + C_1(d) & \text{Understocking cost}\\ C_o(d,q) - C_u(d,q)&= \beta (q -d) &\text{Overstocking cost}\\ \end{align*}\]

Proof: p.68

结论就是： \(Pr(D \le q^*) = {\frac{ \alpha}{\beta}} \)

Other case, if not fit (\(\frac{\alpha}{\beta}\)) - Bidding example

Use General method finding minimum cost (一个普通的最值问题).

---

With Lead time - Continuous Review Models

So now we have two decision variable:

\(q\) quantity ordered each time
\(r\) reorder point

Notation:

\(\begin{align*} K &= \text{Ordering Cost} \\ h &= \text{holding Cost} \\ L &= \text{Lead Time (constain)} \\ D &= \text{Demand/year} \\ X &= \text{Demand during lead time} \\ r - \bar{X} &= \text{safety stock} \\ C_B &= \text{Cost of each unit back-ordered(shortage)} \\ B_r &= max\{0,X-r\} \text{number of units of shortage during a cycle} \\ f(x) &= \text{The distribution of X} \\ \bar{B_r} &= \int^{\infty}_{r}(x-r)f(x) dx \\ & \text{This is a genius part. Putting } r \text{ into the function} \end{align*}\)

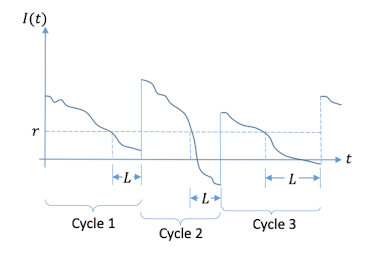
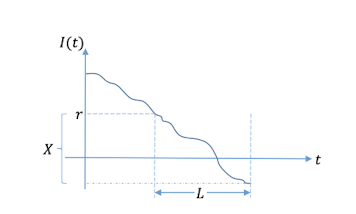
每次库存量触碰 r 的时候，呼叫订单。Cost function:
Note: This cost is $xx /year

\[TC(q,r) = h(r - \bar{X} + q/2) + {\frac{C_B \bar{B_r} \bar{D} }{q} + {\frac{K \bar{D}}{q}}}\] \[\begin{align*} {\frac{ \bar{D}}{q}} &= \text{expected no. of cycles/year} \\ C_B \bar{B_r} &= \text{expected shortage cost/cycle} \end{align*}\]

1. expected holding cost/year. 假设了，整个曲线是线性的，然后让expected inventory = \( {\frac{1}{2}} ([r + q - \bar{X}]\) 初始量 \(+ [r - \bar{X)]}\) 结算量， 这个确实会有误差，即使 \( r - \bar{X} \ge 0\)是肯定成立的(没人会把r设得大几率会产生shortage的情况) 但当L时段的需求大于\( \bar{X}\) ，它是不需要交holding cost的，所以实际是把holding cost高估了。

[2020-04-09] 这门课就是假设shortage的holding cost的影响忽略不计，我花了不少时间查证这个(有时候不懂就要翻翻textbook，自己瞎想容易走火入魔「想不出来容易拖延，干别的(想不出来容易自闭和怀疑自己智商)」，下次问问自己，对这个是不是真的感兴趣，真的感兴趣也要想想有没有时间深入，这个内容是不是真的重要，能不能以后需要用再仔细研究？仔细权衡利弊，做好计划和记录再开始！切记, 有舍有得才是赢家！)

1. expected shortage cost/year.
2. expected ordering cost/year.

\[\begin{align*} {\frac{\partial TC(q,r)}{\partial q}} &= {\frac{h}{2}} - {\frac{C_B \bar{B_r} \bar{D} + K \bar{D}}{q^2}} \\ {\frac{\partial TC(q,r)}{\partial r}} &= h + {\frac{C_B \bar{D}}{q}} \cdot {\frac{d \bar{B_r}}{d r}} \end{align*}\]

结论是: 这是一个二元方程，两个偏导数=0 求解比较麻烦，所以直接让

\[\begin{align*} q^* &= \sqrt{ {\frac{2K \bar{D}}{ h}}}\\ \end{align*}\]

可以解出答案： \(\begin{align*} Pr(X \ge r^*) &= {\frac{hq^*}{C_B \bar{D}}} \\ Pr(X \ge r^*) &= Pr(Z \ge {\frac{r^* - \bar{X}}{\sigma}} ) \end{align*}\)

Note:

1. safety stock \( r^* - \bar{X}\)
2. If \( {\frac{h q^}{C_B \bar{D}}} > 1\), then we cannot use the above formula to determine \( r^\). In this case we simply set r* to a small value. (like epsilon? or negative value?)

N?

For example:

\[\text{ Every year}\\ D \thicksim N(1000, 40.8^2) \\ \text{X is every week, 1/26 year} \\ X \thicksim N( {\frac{1000}{26}} , {\frac{40.8^2}{26}}) \\\] \[\begin{align*} Pr(X\ge r^*) &= Pr(Z\ge {\frac{r^* - {\frac{1000}{26}} }{ {\frac{40.8}{\sqrt{26}}} }}) \\ \end{align*}\]

Lost sale case (Shortage not allow) 短缺的需求不会在未来兑现

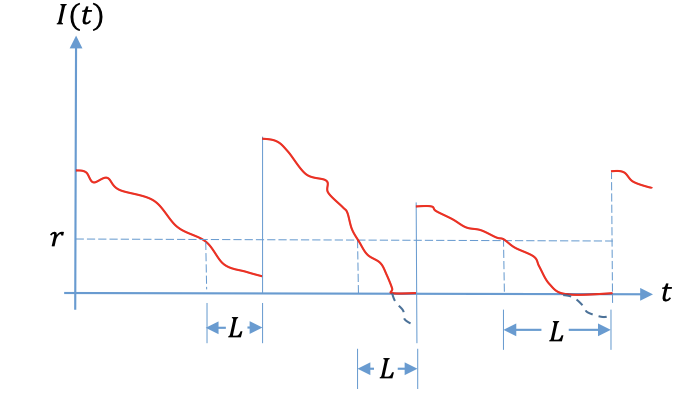
(图里的L为什么不是一样长的，但是我们这个课只讨论是constant的情况。)

Notation:
\( C_{LS} = \) cost of 1 unit of lost sale (already include penalty for loss of future goodwill and profit lost because of lost sale)

Expected inventory level in a cycle: \(\begin{align*} &= (r - \bar{X} + {\frac{q}{2}}) + (expected shoratages/cycle) \\ &= (r - \bar{X} + {\frac{q}{2}}) + \bar{B_r} \\ \end{align*}\)

前半部分和back-logged一样，然后再加一个 \( \bar{B_r}\). 就是说，lost 掉的那部分订单没了，存货多了，相应的库存就增加了。 (这里也顺便验证前面的，课本直接忽略了那部分 库存 \(\le 0\) 的情况)

\(\begin{align*} TC(q,r) &= h(r - \bar{X} + {\frac{q}{2}} + \bar{B_r}) + {\frac{C_{LS} \bar{B_r} \bar{D} }{q}} + {\frac{K \bar{D}}{q}} \\ \end{align*}\) 还是 Holding cost + shortage cost + setup cost。
shortage cost 也是简单的把 \(C_B\) 变成 \( C_{LS}\)

\[\begin{align*} q^* &= \sqrt{ {\frac{2K \bar{D}}{h}}} \\ {\frac{\partial TC(q,r)}{\partial r}} &= h + {\frac{d \bar{Br}}{dr}} (h + \frac{C_{LS}\bar{D}}{q}) \\ Pr(X \ge r^*) &= {\frac{hq^*}{hq^*+C_{LS} \bar{D}}} \end{align*}\]

相比之前的 \(r^*\) 就是分母多了个 \(h q^*\) 项。

(s,S) policies: 补到 S 这么多

之前是简单的补 \(q\) 这么多的货，加上一个条件是，如果需求曲线不是连续的，可能会跳过r点以下，这样就要补更它的差货： \( r^* - I(t)\) 到 \(S\).

Service Level Approach

因为经常，shortage penalty cost 比较难界定，所以会用Service level approach。就只是换了个衡量标准，不再用cost 来衡量。

Service Level measure 1

\(\begin{align*} SLM_1 &= \text{expected fraction of demand met on time.} \\ 1 - SLM_1 &= {\frac{ \text{expected shortages/year}}{ \text{expected demand/year}}} = {\frac{ \bar{B_r} \bar{D} / q}{ \bar{D}}} = {\frac{ \bar{B_r}}{q}} \end{align*}\) 规定，至少% 多少的时间要满足需求。 每个circle，进货 \(q\)， 平均 \( \bar{B_r}\) 的shortage.

Service Level measure 2

用%多少个周期来衡量 \(\begin{align*} SML_2 &= \text{expected number of cycles per year during which a shortage occurs} \\ SML_2 &= \text{(Prob of stockout) x (number of cycles/year).} \\ SML_2 &= Pr(X > r) {\frac{ \bar{D}}{q}} \\ \end{align*}\)

To calculate B_r Normal Loss function

\[\begin{align*} f(x) &= {\frac{1}{\sigma_x \sqrt{2\pi} }} e^{ - {\frac{(x - \bar{X})^2}{2 \sigma_x^2}} } \\ \bar{B_r} &= \int^{\infty}_{r}(x-r)f(x) dx \\ \bar{B_r} &= {\frac{1}{\sigma_x \sqrt{2\pi} }} \int_{r}^{\infty} (x-r) e^{ - {\frac{(x - \bar{X})^2}{2 \sigma_x^2}} } dx \\ &= {\frac{\sigma_x}{\sqrt{2\pi}}} \int_{ {\frac{r - \bar{X}}{\sigma_x}} }^{\infty} (z - {\frac{r - \bar{X}}{\sigma_x}}) e^{ -{\frac{z^2}{2}} } dz \\ NL( \alpha) &= {\frac{1}{\sqrt{2\pi}}} \int_{ \alpha}^{\infty} (z - \alpha) e^{- {\frac{z^2}{2}} } dz \\ \bar{B_r} &= \sigma_x NL( {\frac{r - \bar{X}}{\sigma_x}} ) \end{align*}\]

Then we can check the table of \(NL_{}^{}\) .

Periodic Review Models: (R,S) Policies 定期检查策略

这个策略是假设我们已经决定了 \(R\), 然后我们来找出 \(S\)。

Back-logged case

\(\begin{align*} S &= \text{On-hand inventory + inventory ordered} \\ R &= \text{review interval.}\\ D_{L+R} &= \text{demand during a time interval of length L + R.}\\ E(D_{L+R}) &= {\bar{D}}_{L+R} \text{ std. dev. } \sigma_{D_{L+R}} \text{ } f(x) \\ J &= \text{cost of reviewing inventory level.} \end{align*}\)

简单的说就是，定期查看库存，得到 \(I(t_i)\) 然后补充 \(S - I(t_i)\) 的货到 \(S\). 所以这个model的optimal会比 (r，q) model 更差一些(成本更高)，因为这个model不光固定了，进货量，还固定了了Circle的时长。A more restricted model.

Inventory level in a cycle 库存量

同样是approximate 不用太深究。(期初 + 期末) /2。乍看下面这个表达会让人一头雾水，这么会有 \(\bar{D}_{L+R}\) 这种重复时段的表达呢，其实还是有点微妙的，

\[\begin{align*} &= {\frac{1}{2}} [(S - \bar{D}_{L+R}) + (S - \bar{D}_{L+R} + \bar{D}R)] \\ &= (S - \bar{D}_{L+R} + {\frac{ \bar{D}R}{2}}) \end{align*}\]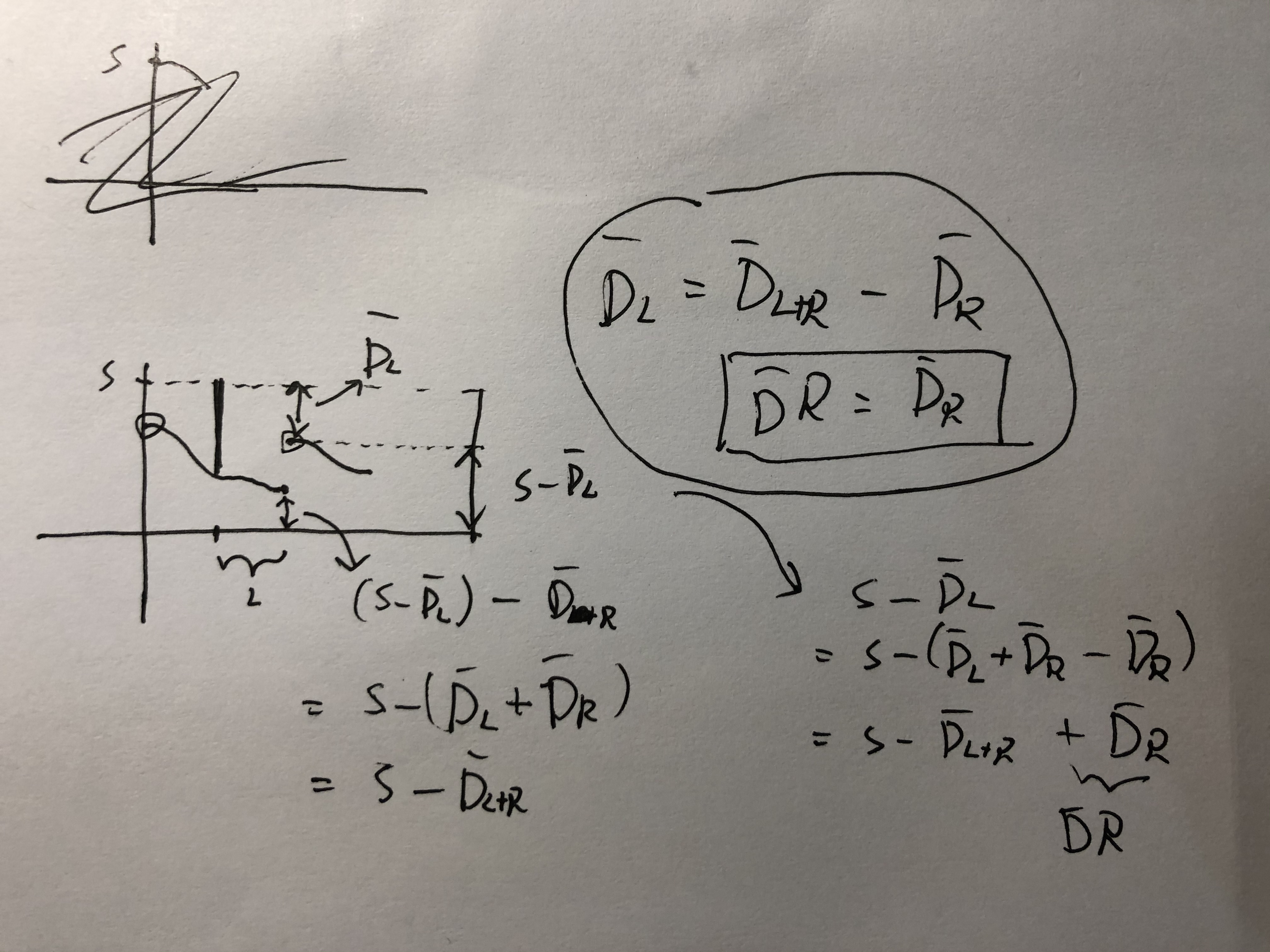

其实这个表达也是有点坑的，但老师的这个note本来就是简略版的，所以就原谅他吧(可能就是想说这个内容并不重要..)

然后顺理成章的，我们有 setup cost + holding cost + expected shortage cost：(cost/year)

\[\begin{align*} TC(R,S) &= {\frac{K+J}{R}} + h[S - \bar{D}_{L+R} + {\frac{ \bar{D}R}{2}}] + {\frac{C_B}{R}} \int_{S}^{\infty} (x-S)f(x) dx \\ \end{align*}\]

先解S，然后conventionally 用EOQ 代q –> \( {\frac{EOQ}{ \bar{D}}} \) 代 \(R_{}^{*}\) (周期长)。

\[\begin{align*} Pr(D_{L+R} > S^*) &= {\frac{Rh}{C_B}} \\ R^* &= {\frac{EOQ}{ \bar{D}}} = \sqrt{\frac{2(K+J)}{h \bar{D}}} \end{align*}\]

Lost-sale case

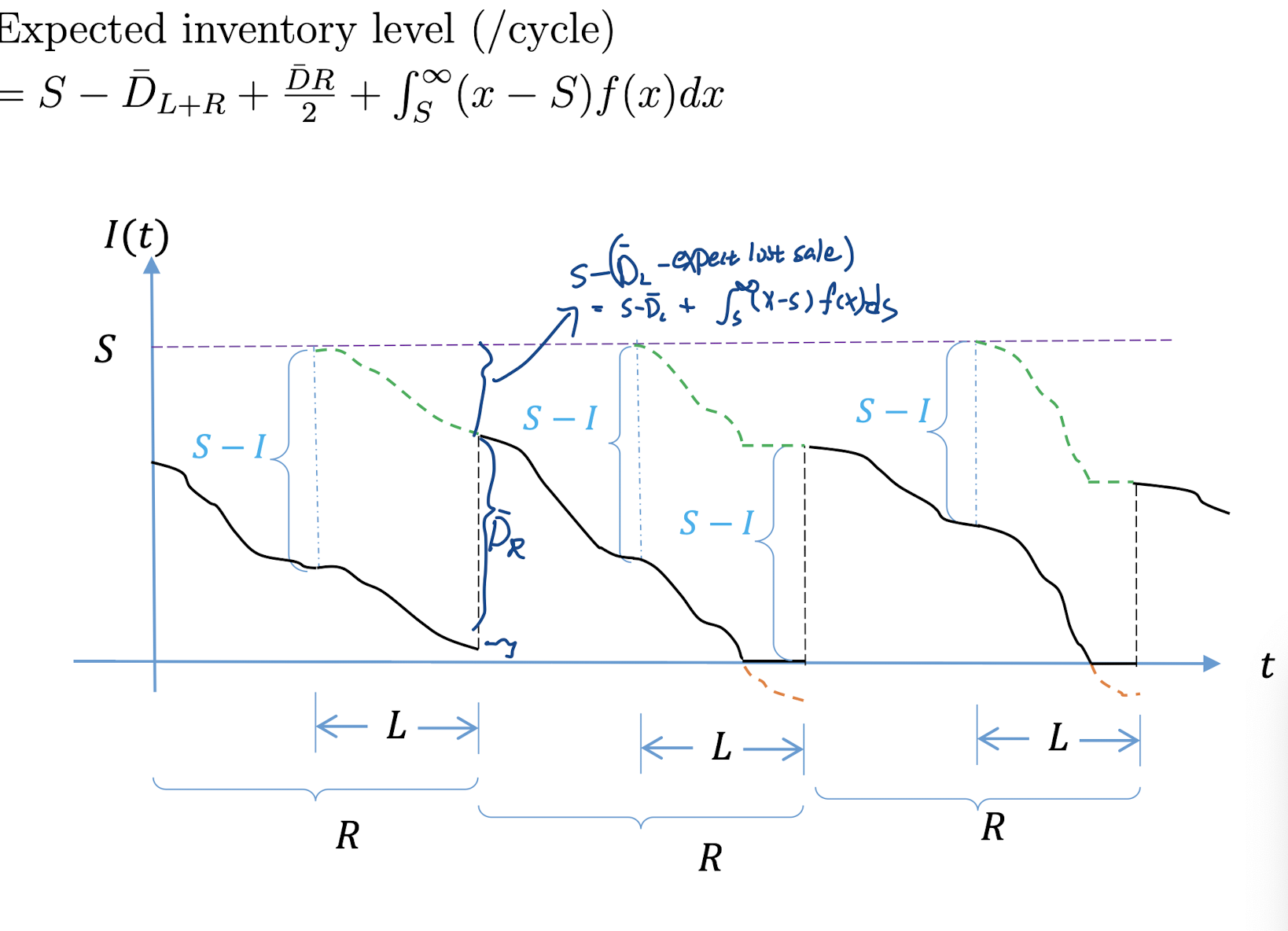
对比 Back-logged case 的expected inventory level, 其实就是多加了一个\( \int_{S}^{\infty} (x-S)f(x) dx\).

所以同理咯，只是全部加一项。

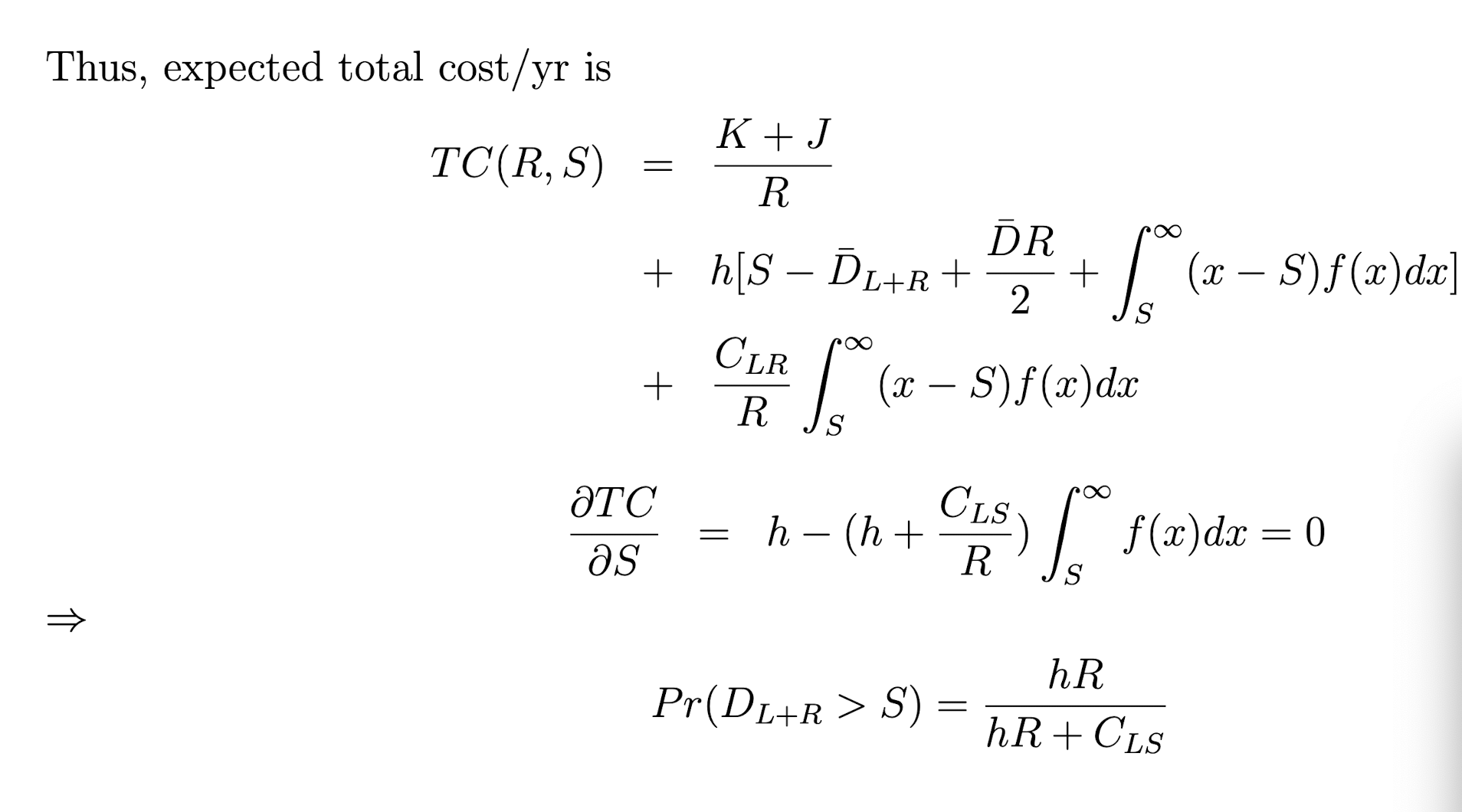
第三部分 Stochastic Programming

General model of two-stage stochastic program.

The introduction example:

\[\begin{align*} x_1 &= \text{wheat (acres of land)} \\ x_2 &= \text{corn (acres of land)} \\ x_3 &= \text{sugar beets (acres of land)} \\ & \\ w_1 &= \text{wheat sold (tons)}\\ w_2 &= \text{corn eat sold (tons)}\\ w_3 &= \text{sugar beets sold (favorable price) (tons)}\\ w_4 &= \text{sugar beets sold (lower price) (tons)}\\ & \\ y_1 &= \text{wheat purchased (tons)}\\ y_2 &= \text{corn purchased (tons)}\\ y_3 &= \text{sugar beets purchased (tons)}\\ \end{align*}\] \[\begin{align*} &\min & 150x_1 + 230x_2 + 260x_3 &\\ & \; &+238y_1 + 210y^2 &\\ & \; &-170w_1 - 150w_2 - 36w_3 - 10w_4 &\\ & & & \\ & s.t.&x_1 + x_2 + x_3 \le 500, &\text{ Total arcs} \\ & \; &\fbox{2.5}x_1 + y_1 - w_1 \ge 200, & \text{ left of wheat minimum, link the yield as well} \\ & \; &\fbox{3}x_2 + y_2 - w_2 \ge 240, & \text{ left of corn minimum, link the yield as well} \\ & \; &w_3 + w_4 \le 20x_3 & \text{ sugar beets less or equal to grow}\\ & \; &w_3 \le 6000, & \text{ good price no exeed quote} \\ & \; & \text{ all variable} \ge 0 & \end{align*}\]

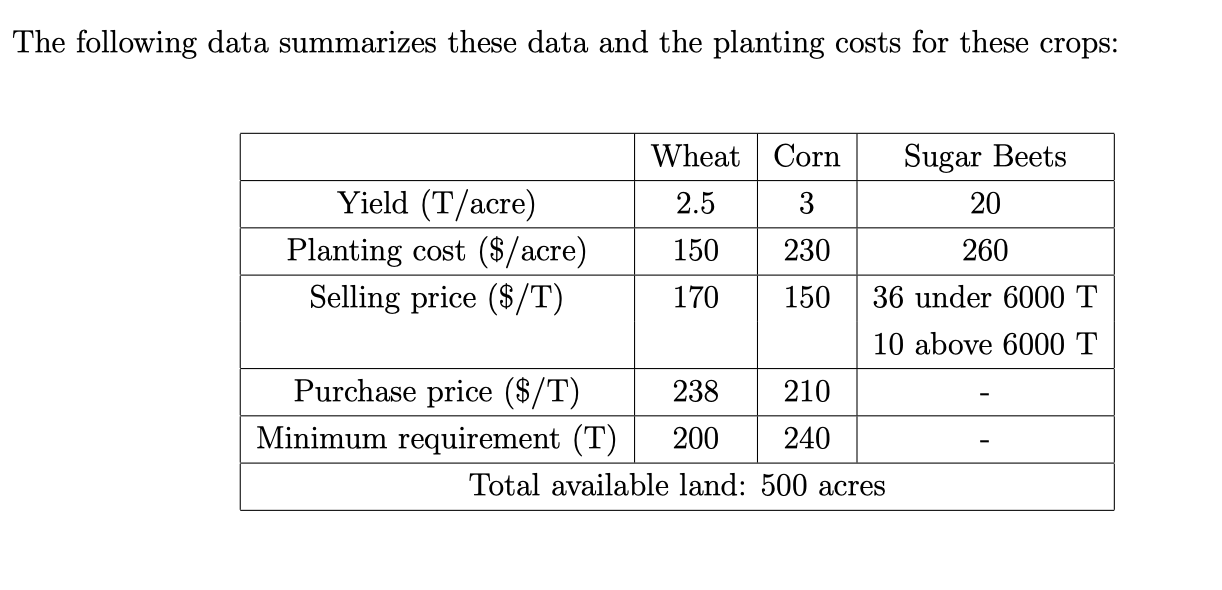
现在问题是，画方块的参数，收成是不确定的，不能保证每亩地的长出的麦子/玉米和以前一样。

所以，假设，有三种情况，低收成，中等收成，高收成，分别是1/3 的概率。

那么我们的variables里的， \(x_1, x_2, x_3\) 不变，但是 \(y, w\) 变成：

\[y_{11}\; y_{12} \;y_{13}\; \text{三种情况的麦子的买入量} \\ w_{11}\; w_{12} \;w_{13}\; \text{三种情况的麦子的卖出量} \\ ...\]

First stage variable: like the arcs.

就像开头的example里的，种多少地，\(x_{1}, x_2, x_3\) 这个是不随收成高低而变化的决策，(种什么是一开始就要确定的)

Second stage variable: The realization of same random vector

像\(y_{11}, y_{12}, y_{13} \) 这种是我们收割完粮食，可以在后面决定的决策。 After full information is received on the realization of some random vector \(\xi\) , the second-stage or corrective actions \(y\in \mathbb{R}^{n2}\) are taken.

General form

\(\begin{align*} &\min c^Tx + \mathbb{E}_\xi Q(x,\xi) \\ &s.t. Ax = b, x\ge 0. \\ \end{align*}\)

\[\begin{align*} Q(x,\xi) &= \min \{\mathbf{q}^Ty| Wy = \mathbf{h}-\mathbf{T}x,y\ge 0 \} \\ \end{align*}\]

所以这里 \(\boldsymbol{\xi}\) 由三个部分组成 \( \boldsymbol{q}, \mathbf{h}, \mathbf{T}\) 是三个random variables可能的，分别对应 c / b / A 三种可能的stochastic的形式。这里的 \(y_{}^{}\) 也是free variable，相等于是后发行动的选择(买卖多少小麦)。

Notation:
a indicator function of a set \( C \subseteq \mathbb{R}^{n}\) \(\begin{align*} \delta_C(x) &= \begin{cases} 0 & \text{ if } x \in C \\ + \infty & \text{otherwise} \end{cases} \\ \end{align*}\)

\[\begin{align*} K_1 &= \{ x| Ax = b, x \le 0 \} \\ K_2(\xi) &= \{ x| \exists y\le 0 \; s.t. Wy = h - Tx \} \\ \end{align*}\]

Then now, we can define cost function: \(\displaystyle \min_{x\in \mathbb{R}^{n_1}} c^Tx + \mathbb{E}_{\xi} Q(x,\xi) + \delta_{K_1}(x)\) 就是，如果这个 \(x_{}^{}\) 不在feasible region的话，optimal是正无穷(infeasible)

\[\begin{align*} z(x,\xi) &= c^Tx + Q(x,\xi) + \delta_{K_1}(x) \\ &= c^Tx + \min \{\mathbf{q}^Ty| Wy = \mathbf{h}-\mathbf{T}x,y\ge 0 \} + \delta_{K_1}(x) \\ & \\ K_2(\xi) &= \{ x| \exists y \le 0 \; s.t. Wy = h - Tx \} \\ \end{align*}\]

K2 同样也可以理解为某种scenario \(\xi\) 里的 feasible region。

所以：

\[\begin{align*} z(x,\xi) &= \begin{cases} + \infty & \text{ if } x \notin K_1 \cap K_2(\xi) \\ - \infty & \text{ if Q is unbounded below} \end{cases} \\ \end{align*}\]

所以最后，two-stage stochastic program can be written as

\[\displaystyle \min_{x\in \mathbb{R}^{n_1}} \mathbb{E}_{\xi} z(x,\xi)\]

The expected Value of Perfect information

Note assumption:

1. There is at least one \(\xi\) that give finite optimal.
2. \( \bar{x}(\xi)\) denotes some optimal solution. with optimal objective value is \(z(\bar{x}(\xi), \xi)\).

“wait and see” (WS) & “here and now” (Recourse Problem RP)

WS: 能遇见未来的情况

RP：更真实的情况

Expected value of perfect information. \(\begin{align*} EV PI &= RP - WS\\ WS &= -\$115,426 ( as {\frac{z_1 + z_2 + z_3}{3}}) \\ RP &= -\$108,390 \text{ 如果不能遇见收成}\\ EV PI &= $7,016\\ \end{align*}\)

Value of the stochastic solution (VSS) (Expected value problem)

\[\begin{align*} &EV &= &\min_{x} z(x, \bar{\xi}) \\ &\bar{x}( \bar{\xi}) &= &\text{the optimal solution of EV} \\ &EEV &= &\mathbb{E}(z(x, \bar{\xi})) \\ &VSS &= &EEV - RP. \text{Value of Stochastic Solution}\\ &WS &\le &RP \le EEV. \\ \end{align*}\]

先用 \(\bar{\xi}\) 确定 \( \bar{x}\)，让后带入 \(z( \bar{x}( \bar{\xi}), \xi)\), 然后再求 \(z_{}^{}\) 的Expectation 这就是为什么有 两个 E.

Example 9.1

WS

EEV

书上其实写的挺清楚的了。直接摘抄了.

\( WS \ge RP \ge EEV\)

proof omit

Benders decomposition

Notation:

\[\begin{align*} &\min_{x, y} &f(x) + h^T y &\\ &s.t. &F(x) + My &\ge b \\ & &x \in \chi, y&\ge 0 \\ & & & \\ & & f, F & \text{ 可能是 non-linear function}\\ & & h^Ty, My & \text{ conventionally 是一个 simple 的linear 问题} \end{align*}\]

然后我们把这个问题拆成两半：

\[\begin{align*} & &\min_{x} & &f(x) + &g(x) \\ & &s.t. & &x \in \chi & \\ & & & & & \\ g(x) &= & \min_{y} & &h^Ty & \\ & & s.t. & &My &\ge b-F(x)\\ & & & &y &\ge 0\\ \end{align*}\]

然后我们取 第二个 Linear 问题的 Dual：

\[\begin{align*} g(x) &= & \max_{u} & &(b-F(x))^Tu & \\ & & s.t. & &M^Tu &\le h\\ & & & &u &\ge 0\\ \end{align*}\]

然后就是非常技术性的一些数学分解, 其实也不难的, 就是需要一点点的耐心～ (简单是不可能简单的, 但是也别怕！)

首先, 一个Linear Problem 的 Feasible Region \(P\) 可以写成这种General 的形式：

\[P = \text{ Feasible Region}\\ p = \text{ 假设有 p 个 extreme points 极值点, 对应} \mu^1, \cdots, \mu^p \\ q = \text{ 假设有 q 个 extreme rays, 对应} d^1, \cdots, d^q \\ \forall u \in P, \; \; u = \sum_{i = 1}^{p} \lambda_i u^i + \sum_{j = 1}^{q} \mu_j d^j \\ \sum_{i = 1}^{p} \lambda_i = 1 \text{ convex hell} \\\]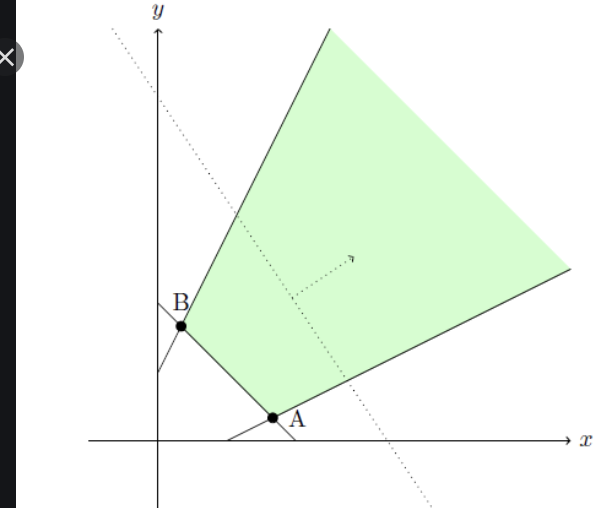

比如这个图, 有 两个 extreme rays, 两个 extreme points : A, B.

所以 把u带入dual LP：

\[\begin{align*} & &\max_{ u \in P} c^T u \\ &= & \max_{1 \le i \le p, 1 \le j \le q} \{ \sum_{i = 1}^{p} \lambda_i c^T u^i + \sum_{j = 1}^{q} \mu_j c^T d^j \} \\ & & \text{ with the convex hall and extreme rays}\\ &= & \begin{cases} + \infty & \text{ if } \exists d^j s.t. c^Td^j > 0 \\ \text{ 如果是 unbounded, (不会是feasible, 前面已经假设了)} \\ \max \{ c^T u^i : i = 1, \cdots, p \} & \text{ if } c^Td^j \le 0, \forall j = 1, \cdots, q. \\ \text{ 至少在 c 的方向是 bounded 的 情况} \end{cases} \\ \end{align*}\]

然后我们再把 \( g(x) \) 代入总的 , (我们又假设了 总的 problem 是 feasible的,) (所以 \( (b - F(x))^T d^j \le 0 , \forall j = 1, \cdots, q\) 算入一个条件里。

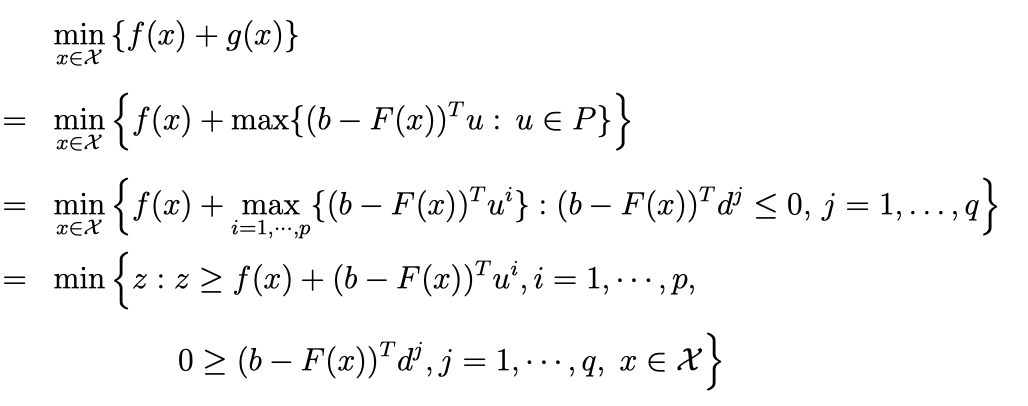
所以现在的问题变成了： Restrict Master Problem

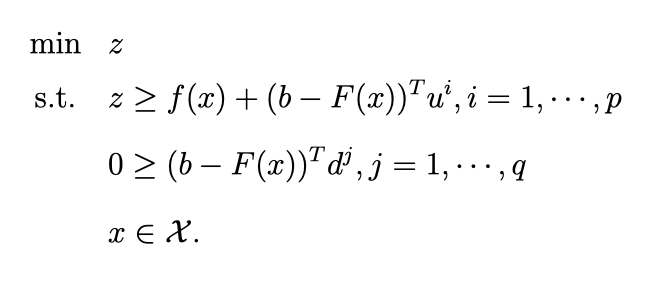
到目前为止其实完全只是 notation 的rewrite ,还没有动用任何高级的知识, 只是相等于把 Linear 的部分简化了。x 的部分还没动。

现在 终于登场了：

The Benders Algorithm

Notation:

\[\begin{align*} L_1 &\subset \{ u^1, \cdots, u^p \} & \text{ Extreme points full sets} \\ L_2 &\subset \{ d^1, \cdots, d^q \} & \text{ Extreme rays full sets} \\ & RMP = & \text{Restricted Master Problem} \end{align*}\]

Extreme Ray Example
比如说：

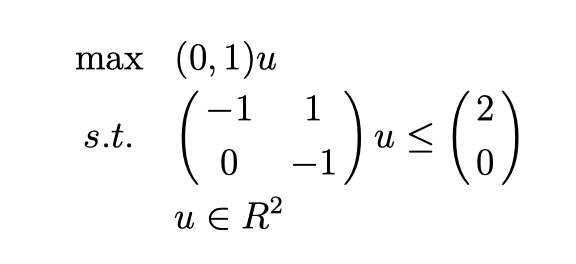
它的图像是这样的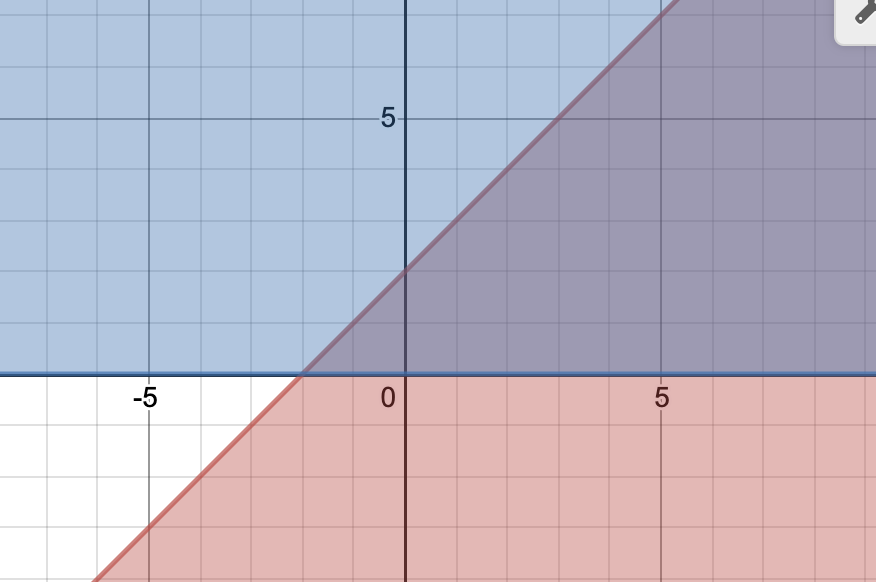： 所以 它的 Extreme ray 有两条: \(\begin{align*} \left(\begin{array}{ccc} 1 \\ 1 \\ \end{array} \right) \end{align*}\) , \(\begin{align*} \left(\begin{array}{ccc} 1 \\ 0 \\ \end{array} \right) \end{align*}\)

它的length 不重要。

Benders’ Master Problem (RMS)

就是那个 z 的 总问题。

Benders’ Subproblem: (is the dual problem of min g(x))

所以很自然的, Primal 是 min , dual 的任一个solution 都是Primal 的Lower bound。 Primal 的任一个 solution都是 Primal 的Upper bound(但这不是重点)

Algorithm:

Initial step: set Lower bound and Upper bound : \( l_b = - \infty, \; u_b = + \infty \) set k:= 0.

Iterative Step: if \( u_b - l_b \ge \epsilon \) , set k = k + 1

1. Solve RMP to obtain \( (x^k, z^k)\), Update \(l_b = z^k \).
2. Solve the dual of the Benders’ 然后有两个情况
   • Case (i) dual is unbounded (无穷大). Primal is infeasible : add a feasibility cut: 就是 肯定存在一个 extreme ray \(d_{}^{j_k}\) such that \((b - F(x^k))^T d^{j_k} \le 0\) ( >0 只要大于0, extreme ray的特点就是可以任意取到无穷) 对应的 我们要它cut 掉, 所以自然的就是让它
   • \( (b - F(x))^T d^{j_k} \le 0\) 同时 (enlarge L2)
   • Case (ii) dual is bounded. 所以 那个最大值一定在Extreme Points, We can add an optimality cut:
   • \( z \ge f(x) + (b- F(x))^T u^{j_k}\) (enlarge L1)
   • Dual 的solution 就是它optimal的一个upper bound: 所以, \( u_b = \min\{ u_b, f(x^k) + (b - F(x^k))^T u^{j_k} \} \)。 这个 upper bound lower bound 很tricky , \( z \le \) something, 我们求的是 z 的最小值, 所以 这个something 应该越来越小, 然后 我们的 z 可以 squeeze 到这个 更小的数, 这就为啥是 upper bound 的意思。
   • We need to meed the minimum upper bound == maximum lower bound