Visual_data

Mathematics for Visual Data Processing 图像处理数学note MA4264

一共有三章:

1. 基础- 函数空间和基
2. 傅立叶
3. 小波理论 Wavalet

Space:

1. Linear Space
2. Linear Spaces with Norm
3. Complete Linear Spaces with Norm ( Banach space)
4. Banach Space with Inner product (Hilbert Space)

\[\begin{align*} L^1(\mathbb{R}) &= \{ f: \int_{0}^{2\pi} |f(x)| dx < \infty \} \\ L^2_{2\pi} &= \{ f: \int_{0}^{2\pi} |f(x)|^2 dx < \infty \} \\ L^2_{[0,T]} &= \{ f: \int_{0}^{T} |f(x)|^2 dx < \infty \} \\ ℓ^p ( \mathbb{Z}) &= \{ x: \| x \|_p < + \infty \} \text{ 小写的L 是 discrete 的 } L^p\\ &= \{ x: ( \sum_{i \in \mathbb{Z}} | x_i|^p)^{ {\frac{1}{p}}}< + \infty \} \\ \end{align*}\]

Notation:

\[\begin{align*} f(x) &= \text{ values of the analog signal function general form} \\ f[n] &= \text{ sample values on n} \\ &= \sum_{p \in \mathbb{Z}} f[p] \delta [n -p]\\ \delta [n] &= \begin{cases} 1 \text{ if } n = 0\\ 0 \text{ otherwise} \end{cases} \\ Lf[n] &= \sum_{p \in \mathbb{Z}} f[p] h [n -p] = (f \ast h) [n]\\ & \text{所以 有 [n] 一般是 sum not integral}\\ L &= \text{ a discrete linear time-invariant operator}\\ h &= \text{ corresponding impluse response filter}\\ \end{align*}\]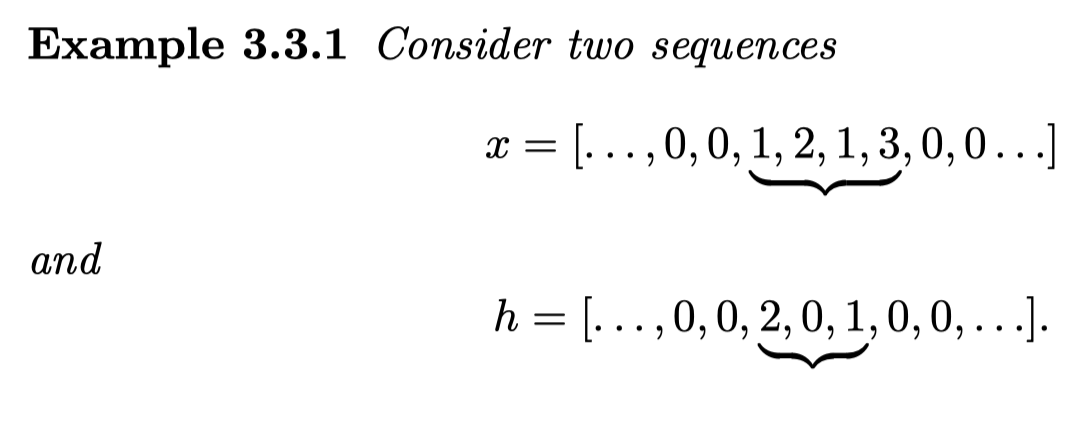

Chapter 1 基础- 函数空间和基

Linear Space with norm

Norm: \(\begin{align*} \| x \|_p &= ( \sum_{n = - \infty}^{ + \infty}) |x_n|^p )^{\frac{1}{p}} \\ \end{align*}\)

Banach space

\(H_{}^{}\) is complete if every Cauchy sequence in H connverges to an element in \(H_{}^{}\). A complete linear space \(H_{}^{}\) is a \(Banach_{}^{}\) space.

Hilbert Space:

Norm

Norm 是这样定义的; \(\begin{align*} \| x \|_2 &= \sqrt{ \langle x,x \rangle } ,\,\, x \in H \\ \end{align*}\)

Remark:

如果 在 复数空间 \(x, y \in \mathbb{C}\)

\[\begin{align*} \langle x,y \rangle &= ( \langle y,x \rangle )^* \\ \end{align*}\]

直接交换律可能不满足。

很简单的例子 Euclidean space \( \mathbb{C}^{n}\)

\[\begin{align*} & \langle x,y \rangle = \sum_{i = 1}^{n} x_i y_i^* \\ &\neq \langle y,x \rangle = \sum_{i = 1}^{n} y_i x_i^* \\ \end{align*}\]

所以我们如果说 Hilbert space 我们一定要先搞清楚它默认定义的 inner product 是什么。

Cauchy-Schwartz inequality

\[| \langle x,y \rangle | \le \| x \| \cdot \| y \| , \,\, \forall x,y \in H.\]

这个证明挺tricky的, 居然是用二次函数的求根证明的：

\[\begin{align*} \langle x + ty, x + ty \rangle &\ge 0 \\ = \langle x,x \rangle + 2t \langle x,y \rangle + t^2 \langle y,y \rangle \ge 0\\ \end{align*}\]

所以, 这可以看成是 对 t 的一个二次函数, 按照定义： \( \langle y,y \rangle \ge 0 \) 这是个开口向上的 抛物线。 所以, 要让它 for all t 恒成立, \( b^2 - 4ac \le 0 \)

\[\begin{align*} b^2 - 4ac &= 4 \langle x,y \rangle ^2 - 4 \langle x,x \rangle \langle y,y \rangle \le 0 \\ &\to | \langle x,y \rangle |^2 - \| x \|_2^2 \| y \|_2^2 \le 0 \\ \end{align*}\]

Proof is done.

Orthonormal sequence in Hilbert space H, equivalent statements:

1. \( { v_n } \text{ is an orthonormal basis in } H \text{ completeness}\)
2. Pareval’s relation \( \langle f,g \rangle = \sum_n \langle f, v_n \rangle \langle g,v_n \rangle , \,\, \forall f,g \in H\)
3. Plancherel’s identity \( | f |^2 = \sum_n | \langle f,v_n \rangle |^2\)

   Chapter 2 傅立叶 Fourier 基

Fourier Series in \(L^2_{2\pi}\)

Notation:

\[\begin{align*} & \{ {\frac{1}{ \sqrt{2\pi} }} e^{int} \}_{ n \in \mathbb{Z}} &= \text{ Fourier Series} \\ \end{align*}\]

Inner Product in \(L^2_{2\pi}\)

\[\begin{align*} \langle f,g \rangle &= \int_{0}^{2\pi} f(x) g^*(x) dx \\ \end{align*}\]

Fourier Series is an orthonormal basis for \(L^2_{2\pi}\)

For any function \( f \in L^2_{2\pi}\)

\[\begin{align*} f(x) &= {\frac{1}{ \sqrt{2 \pi} }} \sum_{n \in \mathbb{Z}} \langle f, {\frac{1}{ \sqrt{2\pi} }} e^{in x} \rangle e^{in x}\\ & = {\frac{1}{2 \pi}} \sum_{n \in \mathbb{Z}} (\int_{0}^{2\pi} f(t) e^{-in t} dt) e^{ i n x} \end{align*}\]

注意 这个 波长 n, 就是简单的 整数？ ( 不是 \(\pi_{}^{}\) 为单位的？ )

确实是, 应该和 \(\pi_{}^{}\) 有关, 只是恰好是 \(L^2_{2\pi}\) 所以抵消了, 下面有更general 的表达式。

Proof is optional

Extension for \(L^2_{[0,L]}\)

所以其实就是简单的 代换, 换scale

Inner Product in \(L^2_{[0,L]}\)

\[\langle f,g \rangle = \int_{0}^{T} f(x) g^*(x) dx\]

\(L^2_{[0,L]}\)Fourier basis

\[\{ {\frac{1}{ \sqrt{T} }} e^{i {\frac{2\pi}{T}} n \omega} \}_{n \in \mathbb{Z}}\] \[\begin{align*} \tilde{f} (x) &= f(x - KT), \forall x \in [kT, (k+1)T]; \,\, k \in \mathbb{Z} \\ & \text{ 推广到了 所有 T periodic 的 函数}\\ \tilde{f} (x) &= \sum_{n \in \mathbb{Z}} \langle \tilde{f} , {\frac{1}{ \sqrt{T} }} e^{i {\frac{2\pi}{T}} n \omega} \rangle {\frac{1}{ \sqrt{T} }} e^{i {\frac{2\pi}{T}} n \omega} \\ \end{align*}\]

所以说, 现在来到了我们的主题： 我们最关注的是, 在\(L^2(\mathbb{R})\) space 的basis 是什么。

??? 首先剧透一下, \(L^2( \mathbb{R})\) 下的 basis 并不存在！ 但是我们还是有一个很好的结果在 \(L^2_{ \mathbb{R}} \cap L^1_{\mathbb{R}}\) 里

原因是, 不是所有的 \( f \in L^2( \mathbb{R})\, \, \int_{- \infty}^{\infty} f(x) e^{-in \omega} dx\) converge absolutely. 比如 \( f(x) = {\frac{ e^{in \omega}}{x}} \)

Fourier transform !

For \( \underline{f \in L^1( \mathbb{R})}\), the Fourier trnasform of \(f_{}^{}\) as \( \widehat{f} : \, \mathbb{R} \to \mathbb{C}\)

\[\begin{align*} \widehat{f}( \omega) &= \int_{ \mathbb{R}} f(x) e^{-ix \omega} dx \\ \end{align*}\]

注意是 在 L1

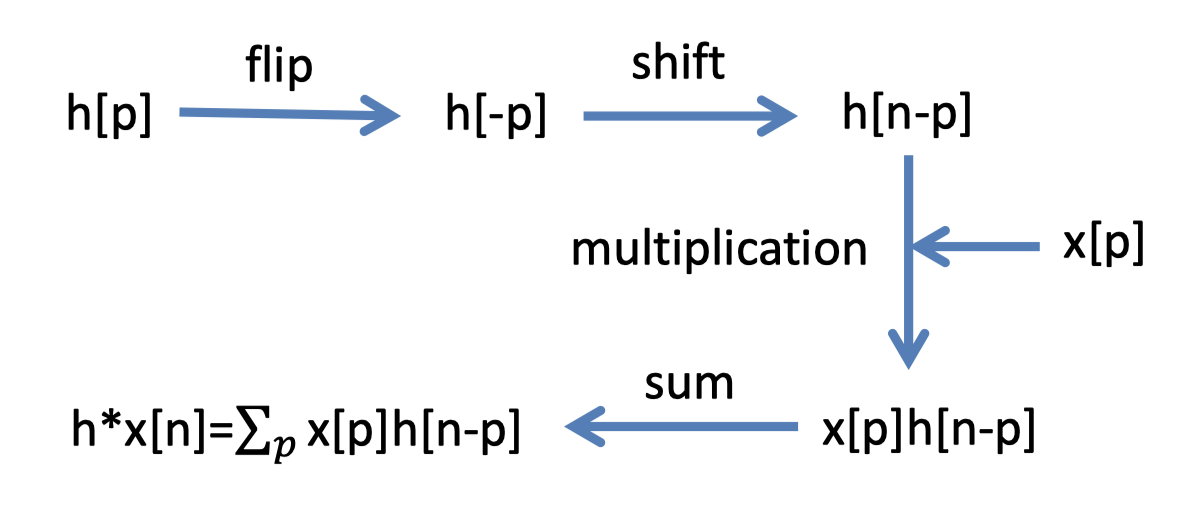
Convolution

\[\begin{align*} \int_{ \mathbb{R}} f(u) g(t - u) du &< \infty \\ (g \ast f) (t) &= \int_{ \mathbb{R}} f(u) g(t - u) du \\ \end{align*}\]

Property:

1. Correlativity: \(f \ast g = g \ast f\)

2. Differentiability \({\frac{d }{d t}} (f \ast g) = {\frac{d f}{d t}} \ast g(t) = f \ast {\frac{d g}{d t}}\)

3. Dirac convolution, \((f \ast \delta_{\tau}) (t) = f(t - \tau).\)

4. Cauchy-Schwarz inequality \(\vert f \ast g \vert \le \| f \|_2 \| g \|_2\).

5. \( | f \ast g |_1 \le | f |_1 | g |_1 \), where \(f, g \in L^1( \mathbb{R})\)

6. \( | f \ast g |_2 \le | f |_1 | g |_2 \), where \(f \in L^1( \mathbb{R})\) and \(g \in L^2( \mathbb{R})\)

Inverse Fourier Transform

\[\begin{align*} f(t) &= {\frac{1}{2\pi}} \int_{ \mathbb{R}} \widehat{f} ( \omega) e^{i \omega t} d \omega \\ \end{align*}\]

Proof:

Fourier Transform property

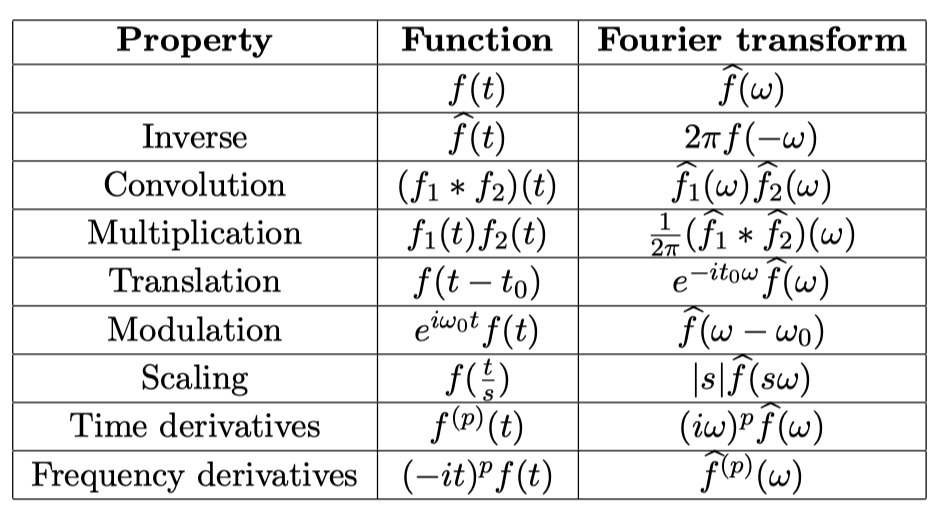
要记忆的特殊情况 1 / sinc

\[\begin{align*} f &= \boldsymbol{1}_{[-T,T]} \\ \widehat{f} ( \omega) &= \int_{-T}^{T} e^{-i \omega t} dt = {\frac{2 sin(T \omega)}{ \omega }} = 2T {\frac{sin (T \omega)}{T \omega}} = 2T sinc (T \omega) \end{align*}\]

反过来的情况

\[\begin{align*} \widehat{h} ( \omega) &= \boldsymbol{1}_{ [- \eta, \eta]} \\ h(t) &= {\frac{1}{2\pi}} \int_{ -\eta}^{\eta} e^{i \omega t} d \omega = {\frac{sin ( \eta t)}{ \pi t }} = {\frac{\eta}{\pi}} sinc( \eta t) . \\ \end{align*}\]

要记忆的特殊情况 Gaussian

Gaussian \(f(t) = e^{- t^2}\) 的 Fourier transform is also a Gaussian

\[\widehat{g} ( \omega) = \sqrt{\pi} e^{ - {\frac{ \omega^2}{ 4}} }\]

这是用 微分方程 求的：

\[\begin{align*} \widehat{f}( \omega) &= \int_{ \mathbb{R}} e^{- t^2} e^{ - i \omega t} dt \text{ 恰好是一个 ode}\\ 2( \widehat{f}( \omega)) \prime + \omega \widehat{f}( \omega) = 0\\ \end{align*}\]

\(\underline{\widehat{g}(- \omega) = \widehat{g}^* ( \omega)}\)

\[\begin{align*} g(t) &\to \widehat{g} ( \omega) \\ g(t) &\to \int_{ \mathbb{R}} g(t) e^{-i \omega t} d t\\ g(-t) &\to \int_{ \mathbb{R}} g(-t) e^{-i \omega t} d t\\ =g(x) &\to \int_{ \mathbb{R}} - g(x) e^{-i \omega (-x)} d x\\ &= -\int_{ \mathbb{R}} g(x) e^{i \omega x} d \\ &= - \boxed{\widehat{g} ( - \omega)} \\ &= - \boxed{(\widehat{g} (\omega))^*} \\ \end{align*}\]

Parseval Formula The 2.3.3

\[\begin{align*} \int_{ \mathbb{R}} f(t) (g(t))^* dt &= {\frac{1}{2\pi}} \int_{ \mathbb{R}} \widehat{f}( \omega) ( \widehat{g}( \omega))^* d \omega \\ \end{align*}\]

Proof:

Set \(h(x) = f( \cdot) \ast g(- \cdot) (x)\)

\[\begin{align*} \widehat{h} ( \omega) &= \widehat{f} ( \omega) \widehat{g}^* ( \omega)\\ h ( t) &= {\frac{1}{2\pi}} \int_{ \mathbb{R}} \widehat{h} ( \omega) e^{i \omega t} d \omega \\ \end{align*}\] \[\begin{align*} h(t) = f \ast g (t) &= \int_{ \mathbb{R}} f(u) g( t - (-u)) du \\ &= \int_{ \mathbb{R}} f(u) g(t + u)) du & \\ h ( t) &= {\frac{1}{2\pi}} \int_{ \mathbb{R}} \widehat{h} ( \omega) e^{i \omega t} d \omega \\ & \\ f \ast g(0) &= \boxed{\int_{\mathbb{R}} f(u) (g(u))^* du} \\ = h(0) &= {\frac{1}{2\pi}} \int_{ \mathbb{R}} \widehat{h} ( \omega) e^{i \omega 0} d \omega\\ &= {\frac{1}{2\pi}} \int_{ \mathbb{R}} \widehat{h} ( \omega) d \omega\\ &= \boxed{ \frac{1}{2\pi} \int_{ \mathbb{R}} \widehat{f}( \omega) ( \widehat{g}( \omega))^* d \omega} \\ \end{align*}\]

The proof is done

Plancherel formular

只是 Parseval 的 \( f = g\) 的情况而已。 \(\begin{align*} \int_{ \mathbb{R}} |f(t)|^2 dt &= {\frac{1}{2\pi}} \int_{ \mathbb{R}} | \widehat{f} ( \omega) |^2 d \omega \\ \end{align*}\)

\(L^2_{ \mathbb{R}}\)

Discrete World!

Context: Notation: 现在我们要对付 不连续的数据：

\[f_d(t) = \sum_{n \in \mathbb{Z}} f(nT) \delta (t - nT)\\\]

每个周期一个数据

对应的 傅立叶转换

\[\begin{align*} \widehat{f}_d( \omega) &= \int_{ \mathbb{R}} \sum_{n \in \mathbb{Z}} f(nT) \delta (t - nT) e^{ - i t \omega} dt \\ &= \sum_{n \in \mathbb{Z}} f(nT) \int_{ \mathbb{R}} \delta ( t - nT) e^{ -i t \omega} dt \\ &= \sum_{n \in \mathbb{Z}} f(nT) e^{-inT \omega} \\ \end{align*}\]

Possion Formula

\[\sum_{n \in \mathbb{Z}} e^{- i n T \omega} = {\frac{2\pi}{T}} \sum_{k \in \mathbb{Z}} \delta ( \omega - {\frac{2\pi}{T}} )\]

证明： 主要就是利用, 两边的函数的周期性 \({\frac{2\pi}{T}}\)

代价于：

\[\sum_{n \in \mathbb{Z}} e^{- in T \omega} = {\frac{2\pi}{T}} \sum_{n \in \mathbb{Z}} \delta ( \omega - {\frac{2\pi k}{T}}) = {\frac{2\pi}{T}} \delta ( \omega ). \,\,\, \forall \,\, \omega \in [ - {\frac{\pi}{T}}, {\frac{\pi}{T}}).\]

为了简化, 我们取 \(u ( \omega) = \sum_{n \in \mathbb{Z}} e^{ - i n T \omega}\). Then for any \(f \in L^2_{[- {\frac{\pi}{T}}, {\frac{\pi}{T}} ]}\) 这也是一个 \({\frac{2\pi}{T}}\) 为周期的函数。

我们有：

\[\begin{align*} (f \ast u) (t) &= \int_{ \mathbb{R}} f( \omega) u (t - \omega) d \omega \\ &= \int_{ \mathbb{R}} f( \omega) \sum_{n \in \mathbb{Z}} e^{ - i n T (t - \omega) } d \omega \\ &= \sum_{n \in \mathbb{Z}} ( \int_{ -{\frac{\pi}{T}}}^{ {\frac{\pi}{T}}}f ( \omega ) e^{ i n T \omega } d \omega) e^{ - i n T t} \\ &= \sum_{n \in \mathbb{Z}} \langle f( \cdot), e^{-inT \cdot} \rangle e^{ - i n T t} \\ \end{align*}\]

然后根据, Orthonormal basis for \(L^2_{[- {\frac{\pi}{T}}, {\frac{\pi}{T}} ]}\)

\[\sqrt{ {\frac{T}{2 \pi}} } \{ e^{-n T t} \}_{n \in \mathbb{Z}}\]

也就是说, 对任意的 f： \(f(t) = {\frac{T}{2 \pi}} \sum_{n \in \mathbb{Z}} ( \int_{ -{\frac{\pi}{T}} }^{ {\frac{\pi}{T}} } f( \omega) e^{ in T \omega} d \omega ) e^{- i n T t}\)

对比刚刚的式子：

\[(f \ast u) (t) = \sum_{n \in \mathbb{Z}} (\int_{ -{\frac{\pi}{T}} }^{ {\frac{\pi}{T}} } f( \omega ) e^{ i n T \omega } d \omega ) e^{ -i n T t} = {\frac{2\pi}{T}}\]

然后又根据 任意 function 和 dirac 的 convolution 等于自身：\(f \ast \delta (t) = f(t)\)

所以总结下前面的过程, 在 \(L^2_{ [-{\frac{\pi}{T}}, {\frac{\pi}{T}}] }\)： \((f \ast u) (t) = {\frac{2\pi}{T}} f(t) = {\frac{2\pi}{T}} (f \ast \delta) (t) \\ \to u = {\frac{2\pi}{T}} \delta\)

Fundamental Lemma

\[\widehat{f}_d ( \omega) = {\frac{1}{T}} \sum_{k \in \mathbb{Z}} \widehat{f}( \omega - {\frac{2k\pi}{T}})\]

Shannon sampling theorem

If the support of \(\widehat{f}\) is included in \([- {\frac{\pi}{T}}, {\frac{\pi}{T}}]\) then

\[f(t) = \sum_{n \in \mathbb{Z}} f(n T) h_T (t - nT)\]

with

\[h_T(t) = T {\frac{sin ( {\frac{\pi t}{T}} )}{\pi T}} = sinc( {\frac{\pi t}{ T}})\]

这就是一个总结, 如何从 sample里还原原function。 注意条件, support of \( \widehat{f}\) 要包含 \([- {\frac{\pi}{T}}, {\frac{\pi}{T}}]\) why？

Chapter 3 小波理论 Wavalet 基

我们要处理的信息是 函数 \(f_{}^{}\) 形式展示的。 所以我们讨论的是整个 \( \mathbb{L}^{2}\) 空间。

Notation:

\[\begin{align*} \{ V_j \}_{j \in \mathbb{Z}^{1}} &= \text{ a sequence of closed subspaces of } \mathbb{L}^{2}( \mathbb{R}) \\ \end{align*}\]

Local time-frequency analysis

Notation:

\[\begin{align*} \Phi &= \{ \phi_r \} \text{ a wave-forms that concentrated in time and in frequency} \\ \| \phi_r \|_2 &= 1. \text{ 假设它的和是1, 即是 概率分布}\\ \Phi (f) (r) &= \langle f, \phi_r\rangle = \int_{ \mathbb{R}} f(t) \phi_r^* (t) dt. \\ = {\frac{1}{2\pi}} \langle \widehat{f}, \widehat{\phi_r} \rangle &= {\frac{1}{2\pi}} \int_{ \mathbb{R}} \widehat{f} ( \omega) \widehat{\phi_r^*} ( \omega) d \omega \text{ 本部分重点公式 Parseval Formula}\\ \end{align*}\]

所以 \( \Phi \)是一个抽象的measure, 注意, 这个 Inner product 虽然不是L2的 baiss 但是也是一种 measure。 只是 如果是 正交基 会完全还原原函数。

Parseval Formula, 其实也是揭露了这个这个物理世界的本质, \(\langle f, \phi_r \rangle\) 相当于是测量它的 位置。 \(\langle \widehat{f} , \widehat{\phi} \rangle\) 相当于是测量它的 动量 (导数)。

\[\begin{align*} u &= \int_{ \mathbb{R}} t | \phi_r (t) |^2 dt \text{ 位置的概率中值} \\ \sigma_t^2 &= \int_{ \mathbb{R}} (t - u)^2 | \phi_r(t) |^2 dt \text{ 位置的 Variance } \\ \eta &= {\frac{1}{2\pi}} \int_{ \mathbb{R}} \omega | \phi_r (\omega) |^2 \omega \text{ 动量的概率中值} \\ \sigma_{ \omega}^2 &= {\frac{1}{2\pi}} \int_{ \mathbb{R}} (\omega - \eta)^2 | \phi_r(\omega) |^2 \omega \text{ 动量的 Variance } \\ \end{align*}\]

比如 Dirac

如果 \(\phi(t) = \delta(t)\)。

\(\begin{align*} \langle f, \delta (t - u) \rangle &= f(u) \\ \langle \widehat{f}, e^{-i u \omega } \rangle &= \int_{ \mathbb{R}} \widehat{f} ( \omega) e^{i u \omega} d \omega\\ \end{align*}\) 所以 neighborhood of \(\widehat{f}\) 给予非常少的information, 除非取 整个 \(\mathbb{R}\) 即 resolution at frequency is very low.

Scaling property & Weyl-Heisenberg’s Uncertainty Principle

\[g(t) = sf(st) \Longleftrightarrow \widehat{g} ( \omega) = \widehat{f} ( {\frac{w}{s}})\]

Theorem:

\[\sigma_t^2 \sigma_{ \omega}^2 \ge {\frac{1}{4}}\]

equality if and only if:

\[f(t) = ( {\frac{2}{\sigma \pi}} )^{\frac{1}{4}} e^{i \xi t} e^{ - {\frac{(t-u)^2}{ \sigma^2}} }\]

Windowed Fourier transform – Gabor

Notation:

\[\begin{align*} \xi &= \text{ frequncy} \\ u &= \text{ translated by u} \\ g(t) &= g(-t) \text{ a real and symmetric windows}\\ g_{u, \xi} &= e^{i \xi t} g(t - u). \\ \| g_{u,\xi} \|_2 &= 1, \forall (u,\xi) \in \mathbb{R}^{2} \text{ normalized}\\ Sf(u,\xi) &= \int_{ \mathbb{R}} f(t) g(t - u) e^{-i \xi t} dt \\ & \text{ S the Windowed fourier transform}\\ \end{align*}\]

所以这和上一个section一样, 都是定义一个抽象的 measure, 这个叫做 Windowed Fourier transform。

\[\begin{align*} g_{u, \xi} &= e^{i \xi t} g(t - u) \\ \widehat{g} (u, \xi) &= \int_{ \mathbb{R}} e^{i \xi t} g(t - u) e^{ - i \omega t} dt \\ &= \int_{ \mathbb{R}} e^{i \xi (t + u)} g(t + u -u) e^{ - i \omega (t+u)} d(t+u) \\ &= \int_{ \mathbb{R}} e^{i \xi (t + u)} g(t) e^{ - i \omega (t+u)} d(t) \\ &= \int_{ \mathbb{R}} g(t) e^{ - i (\omega -\xi) (t+u)} d(t) \\ &= e^{-i u ( \omega - \xi)} \widehat{g}( \omega - \xi)\\ \end{align*}\]

同理,我们 也可以从统计的原理分析它的 Variance \(\begin{align*} \sigma_t^2 &= \int_{ \mathbb{R}} t^2 |g(t)|^2 dt \\ \sigma_{ \omega}^2 &= \int_{ \mathbb{R}} (\omega - \xi)^2 | \widehat{g}_{u, \xi} ( \omega)|^2 d \omega = {\frac{1}{2\pi}} \int_{ \mathbb{R}} \omega^2 | \widehat{g} ( \omega) | d \omega \\ \end{align*}\) 这个是 independent of \((u , \xi)\) 的。

我们现在举几个例子：

Sinusoidal wave

\[\begin{align*} f(t) &= e^{ i \xi_0 t} \\ \text{ 这个的 Fourier transform 是一个 Dirac, 需要记忆的}\\ {\frac{1}{2\pi}} \int_{ \mathbb{R}} \delta (t - \xi_0) e^{ i t \omega } dt &= {\frac{1}{2\pi}} e^{i \xi_0 \omega t} \text{ inverse fourier} \\ \widehat{f}( \omega) &= 2 \pi \delta ( \omega - \xi_0) \\ \end{align*}\]

所以它的 Windows Fourier Transform是

\[\begin{align*} S f(u,\xi) &= \int_{ \mathbb{R}} f(t) g(t -u) e^{ - i \xi t} dt \\ &= \int_{ \mathbb{R}} e^{ i \xi_0 t} g(t -u) e^{ - i \xi t} dt \\ &= \int_{ \mathbb{R}} e^{i \xi_0 t} g(t) e^{ - i \xi ( t + u)} d t \\ &= \int_{ \mathbb{R}} e^{ - i \xi u} g(t) e^{ -i \xi t + i \xi_0 t} dt\\ &= \int_{ \mathbb{R}} e^{ - i \xi u} g(t) e^{ -i (\xi - \xi_0) t } dt\\ &= e^{ - i \xi u} \int_{ \mathbb{R}} g(t) e^{ -i (\xi - \xi_0) t } dt\\ &= e^{ - i \xi u} \widehat{g} ( \xi - \xi_0) \\ \end{align*}\]

Dirac

\[\begin{align*} f(t) &= \delta (t - u_0) \\ S f(u, \xi) &= \int_{ \mathbb{R}} f(t) g(t - u) e^{ - i \xi t} dt\ \ &= \int_{ \mathbb{R}} \delta (t - u_0) g(t - u) e^{ -i \xi t} dt \\ &= g(u_0 - u) e^{ -i \xi u_0} \\ \end{align*}\]

Its energy is spread over the time interval \([ u_0 - {\frac{\sigma_t}{2}} , u_0 + {\frac{\sigma_t}{2}}]\)

Gabor is one type of Windowed Fourier transform

\[g_{u,\xi} = e^{ i \xi t } g(t - u) = e^{i \xi t} e^{ - {\frac{t - u^2}{\sigma^2}} }\]

用的其实是 Gaussian 的内核. 完整的 Gabor system

\[\{ g(t - u_0 j) e^{ i 2 \pi \eta_0 k t} \}_{j,k \in \mathbb{Z}}\]

The only the 1 function forms an Orthonormal basis for \( L^2( \mathbb)\)

Among all the Gabor window, with supp(g) = [0,b] , only one can be the Orthonormal basis. That is

\[g(t) = 1_{[0,1]} (t)\]

“if” <- 1 is an orthonormal basis

我们主要是用的

Plancherel’s identity \(\| f \|^2 = \sum_n | \langle f,v_n \rangle |^2\)

所以我们要求

\[\begin{align*} \| f \|_2^2 &= \int_{ \mathbb{R}} | f(t) |^2 dt = \sum_{j \in \mathbb{Z}} \int_{j}^{j + 1} |f(t)|^2 dt = \sum_{j \in \mathbb{Z}} \| f(t) \boldsymbol{1}_{[j,j+1]} (t) \|_{2}^2 \\ \end{align*}\]

然后我们转到了 每个 \([j, j+1]\) 的小区间。而这个小区间, 我们已经有了 一个basis： for any \(L^2_{[j,j+1]}\) \(\{ e^{i 2 \pi k t} \}_{k \in \mathbb{Z}}\)

所以

\[\begin{align*} \| f(t) \boldsymbol{1}_{[j,j+1]} (t) \|^2 &= \sum_{j \in \mathbb{Z}} | \langle f(t) \boldsymbol{1}_{[j,j+1]}, e^{i 2 \pi k t} \rangle |^2 \\ \end{align*}\]

然后再把每一个部分拼接起来

\[\begin{align*} \| f \|_2^2 &= \sum_{j \in \mathbb{Z}} \sum_{k \in \mathbb{Z}} | \langle f(t) \boldsymbol{1}_{[j,j+1]} (t), e^{i 2\pi kt} \rangle |^2 \\ &= \sum_{j \in \mathbb{Z}} \sum_{k \in \mathbb{Z}} | \langle f(t) g(t - j), e^{i 2\pi kt} \rangle |^2\\ &= \sum_{j \in \mathbb{Z}} \sum_{k \in \mathbb{Z}} | \langle f(t), g(t - j) e^{i 2\pi kt} \rangle |^2\\ \end{align*}\]

这样我们就已经说明了, \(\{ g(t-j) e^{i 2 \pi k t} \}_{k \in \mathbb{Z}}\) 这是一个 Orth basis了。

” only if” an orthonormal basis -> must be 1

已知有, \(\{ g(t-j) e^{i 2 \pi k t} \}_{k \in \mathbb{Z}}\) 是一个 orth basis

First, 我们要先证明 support 是 [0, 1]

\(g(t), g(t-1)\) 是basis 里的成员, 根据正交的属性, 有 \(\langle g(t), g(t-1) \rangle = \int_{ \mathbb{R}} g(t)g(t-1) dt = 0\)

因为我们的, g 的设定就是 恒 \(\ge 0\) 的。所以如果 b>1 我们这个 inner product 就不会为 0 了,

如果 b < 1 , 那就相当于, 这个basis 有空隙, 没办法 complete 所以也不能构成 orth basis。

如此, b 只能为 1 。

(其实这个结果也是显然的, k 取得是全体整数, 如果它不是整数, 或者是 偶数, b也不一样)

然后 我们取 两个 不同的基 作inner product

\[\begin{align*} \langle g(t) e^{i 2 \pi k t}, g(t) e^{i 2 \pi j t} \rangle &= 0 \\ = \langle |g(t)|^2 , e^{ i 2 \pi (j -k) t} \rangle & \;\;\;\, j - k = n \text{ 所以 n 可以是不为0 的任意整数 ( j != k )}\\ = \int_{0}^{1} |g(t)|^2 e^{-i 2\pi n t} dt & \text{ 因为support 是 0-1} \\ \end{align*}\]

恰好, \(\{ e^{i 2 \pi n t } \}_{n \in \mathbb{Z}}\) 是 一个 \( L^2_{[0,1]}\) 的 orth basis 所以, 既然 for any \( n \ne 0\) 都成立, \(\vert g(t)\vert ^2 = e^{i 2\pi 0 t} = 1\)

proof done

Wavelet transform

前面的做法有一个问题, 就是它不管sample function的情况, 它是一个fixed的 window 和 固定的 frequency 集去测量它。

Wavelet 就是这样一个improve, 它先decompose 出不同的 frequency 然后去用不同的basis去度量。

\[W f(u,s) = \int_{ \mathbb{R}} f(t) \psi_{u,s}^* (t) dt = \int_{ \mathbb{R}} f(t) {\frac{1}{ \sqrt{s} }} \psi^* ( {\frac{t - u}{s}} ) d t \\ \{ \psi_{j,n} (t) = {\frac{1}{ \sqrt{2} }} \psi ( {\frac{t - 2^j n}{2^j}} ) \}_{j,n \in \mathbb{Z}} \text{ 这只是其中一个 example}\]

Multi-resolution analysis

1. \[\forall (j,k) \in \mathbb{Z}^{2}, V_j \Longleftrightarrow f(t - 2^jk) \in V_j\]
2. \[\cdots \subset V_2 \subset V_1 \subset V_0 \subset V_{-1} \subset \cdots \text{下标数字越小, 越是基底, 包含越多的信息。}\]
3. \[\forall j \in \mathbb{Z}, f(t) \in V_j \Longleftrightarrow f(2t) \in V_{j-1} \text{ 每一层, 恰好是下一层压缩 1/2}\]
4. \[\lim_{j \to +\infty} V_j = \cap_{j = - \infty}^{+ \infty} V_j = \emptyset\]
5. \[\lim_{j \to -\infty} V_j = \cup_{j = - \infty}^{+ \infty} V_j = \mathbb{L}^{2}( \mathbb{R})\]
6. \[\exists \phi \in \mathbb{L}^{2}(\mathbb{R}) s.t. \{ \phi(t -n) \}_{n \in \mathbb{Z}} \text{ is an orthonormal basis of } V_0. \\ \phi \text{ is called } scaling \, function\]

第三点, \( V_n\) 的 n越小, 就是说, 这个function 越细腻, 越密。分辨率 resolution 越高。 用 \( 2^{-j}\) 表示。

所以 第六点,是我们专门定义一个 \(\phi\) scaling function 作为 \(V_{0}^{}\) 的 正交基。

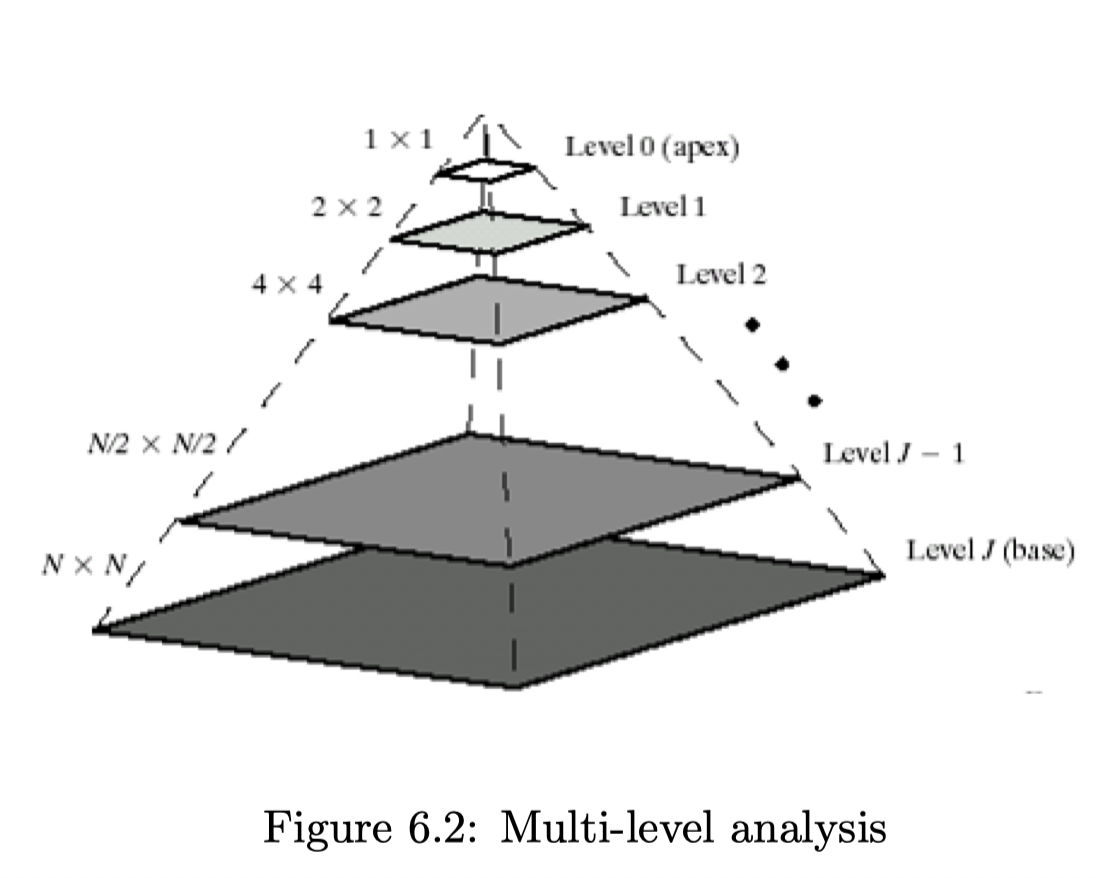
Orthonormal basis of \( V_j\)

\(\phi_{j,n} = \sqrt{ {\frac{1}{2^j}}} \phi ( {\frac{t}{2^j}} -n) \\ \{\phi_{j,n}\}_{ n \in \mathbb{Z}} \text{ is an orthonormal basis of } V_j\)

这个意味着, 我们如果定义了 \(V_{0}^{}\) 的正交基底, 很容易就可以写出其它的 \(V_{j}^{}\) 的正交基。

\( {\frac{t}{2^j}} \) 很容易理解, 但是 前面为什么要有 \( \sqrt{ {\frac{1}{2^j}}} \) 呢

重复一下定义：如果 \(f(t) \in V_0\) 第六个property：

\[\begin{align*} f(t) &= \sum_{n \in \mathbb{Z}} \langle f(t), \phi(t-n) \rangle \phi (t - n) \end{align*}\]

联系到 \( V_j\)

\[\begin{align*} g(t) &\in V_j \\ g(2^j t) &\in V_0 \text{ by property 3}\\ g(2^j t) &= \sum_{n \in \mathbb{Z}} \langle g(2^j t), \phi(t-n) \rangle \phi (t - n) \\ \text{ set } & g(2^j t) = g(x) \\ \end{align*}\]

所以 set \(g(2^j t) = g(x)\), \(x = 2^j t \\ t = {\frac{x}{2^j}}\)

注意：

\[\begin{align*} & \langle g(2^j t),\phi (t - n) \rangle &\neq & &\langle g(x), \phi( {\frac{x}{2^j}}- n) \rangle \\ &= \int_{ \mathbb{R}}^{} g(2^j t) \phi(t - n) dt &\neq & & = \int_{ \mathbb{R}}^{} g(2^j t) \phi({\frac{x}{2^j}} - n) dx \\ &= \int_{ \mathbb{R}}^{} g(x) \phi( {\frac{x}{2^j}} - n) d {\frac{x}{2^j}} & & & \\ &= {\frac{1}{2^j}}\int_{ \mathbb{R}}^{} g(x) \phi( {\frac{x}{2^j}} - n) d x & & & \\ &= {\frac{1}{2^j}}\langle g(x), \phi( {\frac{x}{2^j}} - n) \rangle & & & \\ &= {\frac{1}{2^j}}\langle g(\cdot), \phi( {\frac{\cdot}{2^j}} - n) \rangle & & & \\ \end{align*}\]

所以 代入 \( g( 2^j t) = g(x)\)

\[\begin{align*} g(x) &= \sum_{n \in \mathbb{Z}} \langle g( 2^j t), \phi( (t -n) \rangle \phi (t - n) \\ g(x) &= \sum_{n \in \mathbb{Z}} {\frac{1}{2^j}} \langle g(x), \phi( {\frac{x}{2^j}} - n) \rangle \phi (t - n) \\ g(x) &= \sum_{n \in \mathbb{Z}} \langle g(x), \sqrt{\frac{1}{2^j}} \phi( {\frac{x}{2^j}} - n) \rangle \sqrt{\frac{1}{2^j}}\phi (t - n) \\ \end{align*}\]

而且, \( | \phi_{j,n} |_2^2 = 1 \)

\[\begin{align*} \| \phi_{j,n} \|_2^2 &= \int_{ \mathbb{R}} [\sqrt{ {\frac{1}{2^j}}} \phi ( {\frac{t}{2^j}} -n)]^2 dt \\ &= \int_{ \mathbb{R}} [ {\frac{1}{2^j}} |\phi ( {\frac{t}{2^j}} -n)|^2] dt \\ &= \int_{ \mathbb{R}} |\phi ( {\frac{t}{2^j}} -n)|^2 d {\frac{t}{2^j}} \\ &= \int_{ \mathbb{R}} |\phi (t -n)|^2 dt \\ &= 1 \text{ 本来它就是一个 Orthonormal basis 所以是1} \\ \end{align*}\]

所以很自然的 我们得到了结论： \(\phi_{j,n} = \sqrt{ {\frac{1}{2^j}}} \phi ( {\frac{t}{2^j}} -n) \,\,\, \{\phi_{j,n}\}_{ n \in \mathbb{Z}} \text{ is an orthonormal basis of } V_j\)

和 卷积的联系

\(\begin{align*} \langle g(x), \phi( {\frac{x}{2^j}} - n) \rangle &= \int_{ \mathbb{R}} g(x) \sqrt{ {\frac{1}{2^j}}} \phi( {\frac{x}{2^j}} - n) dx \\ \end{align*}\) ???

和 Fourier 的关系

Notation:

\[\begin{align*} \widehat{\phi} & \in L^2 ( \mathbb{R}) \text{ 假设} \\ & \text{ 且 }\phi(t - n)_n \text{ 是一个 orthonormal sequence}\\ \Psi ( \omega) &= \sum_{k \in \mathbb{Z} } | \widehat{\phi} ( \omega + 2k\pi) |^2 = 1 , \forall \omega \in \mathbb{R} \\ \end{align*}\]

Property： \(\Psi ( \omega) = 1 , \forall \omega \in \mathbb{R}.\)

Proof:

由于我们可以把它看成 \( 2 \pi \) Periodic function, 我们可以用 傅立叶基, 我们可以把它分解成这种形式. \(\begin{align*} \Psi ( \omega) &= \sum_{n \in \mathbb{Z}} {\frac{1}{2\pi}} \langle \Psi( \omega), e^{in \omega} \rangle e^{in \omega} \\ \end{align*}\)

So in \( L^2_{ 2 \pi}\), 就是每一段搞一次

\[\begin{align*} \langle \Psi( \omega), e^{in \omega} \rangle &= \int_{ - \pi}^{ \pi} \Psi ( \omega) e^{-in \omega} d \omega \\ &= \int_{ -\pi}^{\pi} \sum_{k \in \mathbb{Z} } | \widehat{\phi} ( \omega + 2k\pi) |^2 e^{-in \omega} d \omega \\ &= \int_{ -\pi}^{\pi} | \widehat{\phi} ( \omega) |^2 e^{- i n \omega} d \omega\\ & \,\,+ \int_{ -\pi}^{\pi} | \widehat{\phi} ( \omega + 2\pi)|^2 e^{- i n \omega} d \omega \\ & \,\, \vdots \\ &= \int_{ \mathbb{R}} | \widehat{\phi} ( \omega) |^2 e^{- i n \omega} d \omega \\ &= \int_{ \mathbb{R}} \widehat{\phi} (\widehat{\phi} e^{ i n \omega})^* d \omega \text{ Translation & Plancherel Formula}\\ &= 2\pi \int_{ \mathbb{R}} \phi (t) \phi( t +n) dt \\ &= 2\pi \langle \phi(t), \phi(t + n) \rangle \\ \end{align*}\]

因为前面假设, \(\{ \phi(t -n) \}_n\) 是 orthonormal sequence, 所以

\[\begin{align*} \Psi ( \omega) &= \sum_{n \in \mathbb{Z}} {\frac{1}{2\pi}} \langle \Psi( \omega), e^{in \omega} \rangle e^{in \omega} \\ &= \sum_{n \in \mathbb{Z}} {\frac{1}{2\pi}} 2\pi \langle \phi(t), \phi(t + n) \rangle e^{i n \omega} \\ &= 1 e^{ i 0 \omega}\\ &= 1\\ \end{align*}\]

Now its done.

Refinable function

这里就只是一个定义, 它的目的是展示, the scaling function \(\phi\) 也是一个 refinable function. 而 refinable function 是一个非常重要的属性, 它让 \( V_0\) 到\( V_1\) 可以很好的过渡, 就是一次 Convolution 的运算就完成了.

If there exists a sequence \( h\in ℓ^2(\mathbb{Z})\) such that

\[{\frac{1}{ \sqrt{2} }} \phi ({\frac{t}{2}}) = \sum_{n \in \mathbb{Z}} h[n] \phi(t-n)\]

The sequence of h is called the refinement mask of \(\phi\).

前面定义的： \(\{ {\frac{1}{ \sqrt{2}}} \phi ( {\frac{t}{2}} - n)\}_{n \in \mathbb{Z}} \text{ 是 V1 的 正交基}\)

所以

\[\begin{align*} {\frac{1}{ \sqrt{2}}} \phi ( {\frac{t}{2}}) &\in V_1 \subset V_0\\ & \text{ 用 } V_0 \text{ 的基去表示}\\ {\frac{1}{ \sqrt{2} }} \phi ({\frac{t}{2}}) &= \sum_{n \in \mathbb{Z}} h[n] \phi(t-n) \text{ 这个恰好是 convolution 的表达}\\ &= h \ast \phi (t)\\ & \\ & \text{ 两边同时 Fourier Transform}\\ \sqrt{2} \widehat{\phi} (2 \omega) & = \widehat{h}( \omega) \widehat{\phi} ( \omega)\\ \end{align*}\] \[\begin{align*} h [n] &= \langle {\frac{1}{ \sqrt{2}}} \phi ( {\frac{t}{2}}) , \phi(t-n) \rangle \\ \widehat{h} ( \omega) &= \sum_{n \in \mathbb{Z}} h[n] e^{-i n \omega } \\ \end{align*}\]

所以, \(h[n]\) 是存在, 且等于 这个 inner product. 这一部分的目的就是为了引入 h, 来表达 \( V_0 \) 和 \(V_1\) 之间的关系。

注意 这个 Convolution 时而是 sum 时而是 integral, 注意区分

特性 6.1.5

\[\begin{align*} | \widehat{h} ( \omega) |^2 + | \widehat{h} ( \omega + \pi) |^2 &= 2 \\ \end{align*}\]

Proof

前面证明的一个性质

\[\begin{align*} \Psi ( \omega) &= \sum_{k \in \mathbb{Z} } | \widehat{\phi} ( \omega + 2k\pi) |^2 = 1 , \forall \omega \in \mathbb{R} \\ & \Updownarrow \\ \Psi ( {\frac{\omega}{2}} ) &= \sum_{k \in \mathbb{Z} } | \widehat{\phi} ( {\frac{\omega}{2}} + 2k\pi) |^2 = 1 , {\frac{\omega}{2}} \in \mathbb{R} \\ \end{align*}\] \[\begin{align*} \because \sqrt{2} \widehat{\phi} (2 \omega) & = \widehat{h}( \omega) \widehat{\phi} ( \omega)\\ \therefore \widehat{\phi} (2 \omega) & = {\frac{1}{\sqrt{2}}} \widehat{h}( \omega) \widehat{\phi} ( \omega)\\ &\\ \sum_{k \in \mathbb{Z} } | \widehat{\phi} ( \omega + 2k\pi) |^2 &= \sum_{k \in \mathbb{Z}} {\frac{1}{2}} | \widehat{h}( {\frac{ \omega}{2}} + k\pi) \widehat{\phi} ({\frac{ \omega}{2}} + k \pi) |^2 = 1 \\ & \Updownarrow \\ & \sum_{k \in \mathbb{Z}} | \widehat{h}( {\frac{ \omega}{2}} + k\pi)|^2 |\widehat{\phi} ({\frac{ \omega}{2}} + k \pi) |^2 = 2 \\ \end{align*}\]

因为我们前面的性质的前提是 \( 2 \pi \) periodic. 所以可以技术性的把它分开

\[\begin{align*} & \sum_{k \in \mathbb{Z} } | \widehat{h}( {\frac{ \omega}{2}} + 2k\pi)|^2 |\widehat{\phi} ({\frac{ \omega}{2}} + 2k \pi) |^2 + \sum_{k \in \mathbb{Z} } | \widehat{h}( {\frac{ \omega}{2}} + \pi + 2k\pi)|^2 |\widehat{\phi} ({\frac{ \omega}{2}}+ \pi + 2k \pi) |^2\\ & \text{然后} \widehat{\phi} \text{ 直接可以= 1}\\ & = \sum_{k \in \mathbb{Z} } |\widehat{h}( {\frac{ \omega}{2}} + 2k\pi)|^2 + \sum_{k \in \mathbb{Z} } |\widehat{h}( {\frac{ \omega}{2}} + \pi + 2k\pi)|^2 \\ \end{align*}\]

最后由于 \(\widehat{h} ( \omega) = \sum_{k \in \mathbb{Z} } h[k] e^{-in \omega }\) 是 \( 2\pi \) periodic 所以 proof done.

\[\sum_{k \in \mathbb{Z} } |\widehat{h}( {\frac{ \omega}{2}})|^2 + \sum_{k \in \mathbb{Z} } |\widehat{h}( {\frac{ \omega}{2}} + \pi )|^2 = 2 \\\]

这个到底有什么用呢？

the whole orthonormal basis

Notationn

\[\begin{align*} \widehat{\psi} ( \omega) &= {\frac{1}{ \sqrt{2} }} \widehat{g} ( {\frac{ \omega}{2}}) \widehat{\phi} ( {\frac{ \omega}{2}}) \\ \widehat{g} ( \omega) &= e^{-i \omega} \widehat{h}^* ( \omega + \pi) \\ h &= \text{ corresponding filter of } \phi \\ \end{align*}\]

basis： \(\{ \psi_{j,n} (t) \}_{j,n \in \mathbb{Z} = \{ {\frac{1}{ \sqrt{2^j} }} \psi( {\frac{t - 2^jn}{2^j}}) \}_{i,j \in \mathbb{Z}}\)

这门课不要求这个怎么来的, 但要记住这个：

\[g[n] = (-1)^{1-n} h[1-n]\]

更general 的形式：

\[\phi_{j,n} = \sum_{l} h_{l - 2n} \phi_{j-1,l} \psi_{j,n} = \sum_{l} g_{l - 2n} \phi_{j-1,l}\]