Game_thory

Game Theory 博弈论 note

一共有四章:

Definition:

Notation

\[\begin{align*} S_1,...,S_n &= \text{strategy spaces} \\ s_1 &= \text{one selection of player 1's strategy} s_1 \in S_1. \\ s &= (s_1,...,s_{i-1},s_i,s_{i+1},...,s_n) = (s_i, s_{-1})\\ s_{-1} &= (s_1,...,s_{i-1},s_{i+1},...,s_n) \\ S_{-1} &= S_1 \times \cdots \times S_{i-1} \times S_{i+1} \times \cdots \times S_n \\ u_1,...,u_n &= \text{payoff functions} \\ u_i(s_1,...,s_n) &= \text{the payoff value for player i, if s_1..} \\ Game\; G &= \{ S_1,...,S_n;u_1,...,u_n \} \\ \end{align*}\]

Strictly dominated

Strategy \({s_i^\prime}\) is strictly dominated by strategy \(s_i^{\prime\prime}\) if :

\[\begin{align*} u_i({s_i^\prime},s_{-i}) &< u_i({s_i^{\prime\prime}},s_{-i}), \;\; \forall s_{-i} \in S_{-i}. \\ \end{align*}\]

Best Response

The best response for player \(i\) to the other player’s strategies \(s_{-i} \in S_{-i}\) is: \(\begin{align*} R_i(s_{-i}) &= \max_{s_i\in S_i} u_i(s_i,s_{-i}). \\ R_i(s_{-i}) &\subset S_i \text{ it's a set, can be empty, finit or infinite set}\\ \end{align*}\)

Nash equilibrium

Definition 4: In the n-player normal-form game \( G = \{S_1,…,S_n; u_1,…,u_n\} \) the strategies \( (s_1^*, …, s_{n}^*) \) are a Nash equilibrium if

\[\begin{align*} s_i^* &= R_i(S_{-i}^*) \; \; \forall i = 1,...,n, \\ &\iff \\ u_i(s_i^*, s_{-i}^*) &= \max_{s_i \in S_i} u_i(s_i, s_{-i}^*)\; \; \forall i = 1,...,n \end{align*}\]

Graph

\(G(R_i) \) denote the graph of \(R_i \), defined by:

\[\begin{align*} G(R_i) &= \{ (s_i,s_{-i})| s_i \in R_i(s_{-i}), s_{-i} \in S_{-i} \} \\ (s_1^*, ..., s_{n}^*) &\in \cap_{i = 1}^n G(R_i)\\ \end{align*}\]

So to find Nash equilibria

Measure 1 Direct guess

For any guess (\(s_{1}^{*}\),\(s_{1}^{*}\)) \(\in S_1 \times S_2\), compute the \(R_{1}^{}(s_2^*)\) and \(R_{2}^{}(s_1^*)\). Then (\(s_{1}^{*}\),\(s_{1}^{*}\)) is a Nash equilibrium if \( s_1^* \in R_1(s_2^*) \) and \(s_2^* \in R_2(s_1^*) \).

Measure 2 Intersection of the graph

\( (s_1^*, s_2^*) \in G(R_1) \cap G(R_2)\)

1. 完全信息-静态博弈
2. 完全信息-动态博弈
3. 不完全信息-静态博弈
4. 不完全信息-动态博弈
5. 合作博弈

Chapter 1 完全信息 静态博弈

Chapter 2 完全信息 动态博弈

Subgame-Perfect

有两个地方出现了这个 Subgame-Perfect

1. Subgame-Perfect Outcome
2. Subgame-Perfect Nash Equilibrium

Subgame-Perfect Outcome

课件没有给具体的定义,只有几个example..

我理解的就是直接把每个subgame 找出来,然后把每个combine 每个subgame的NE。

Subgame-Perfect Nash Equilibrium

A Nash equilibrium is 'subgame-perfect' if the players' strategies consitute a Nash equilibrium in every subgame .

Infinitely repeated games

The present value of the sequence of payoffs

\[\begin{align*} \pi_1 + \delta \pi_2 + \delta^2 \pi_3 + \dots &= \sum_{t = 1}^{ \infty} \delta^{t-1} \pi_t.\\ 1 + \delta + \delta^2 + \dots &= {\frac{1}{1- \delta}} \\ \delta + \delta^2 + \dots &= {\frac{\delta}{1- \delta}} \\ \end{align*}\]

Trigger strategy \( T_i\)

The Prisoners’ Dilemma Example:

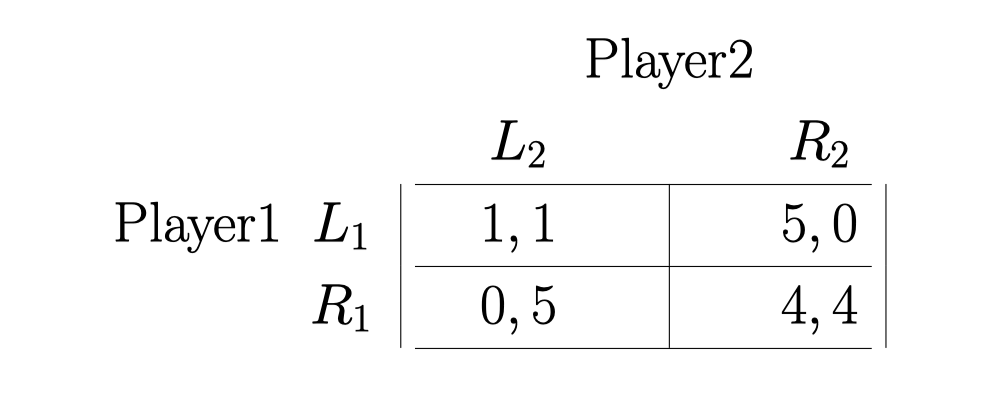
\(R_{}^{}\) is cooperate move, \(L_{}^{}\) is Non-Cooperate move.

现在我们要对比合作还是不合作两种策略： 如果一直合作： \(4 + 4 \delta + + 4 \delta^2 + \dots = {\frac{4}{1- \delta}}\)

如果从,某个时刻开始不合作：

\[5 + \delta \cdot 1 + \delta^2 \cdot 1 + \dots = 5 + {\frac{ \delta}{1 - \delta}}\]

对比就可以解得, \( \delta\) 在什么 范围, 大家会一直合作(Trigger strategy is an Nash equilibrium)

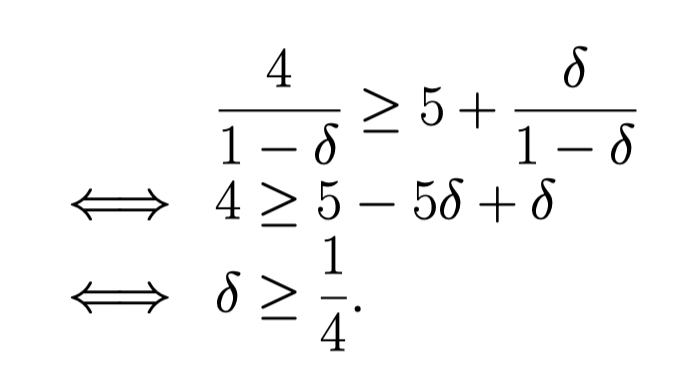
\( {\frac{1}{4}}\) 什么水平？ 折现率是每年25%, 今年1块钱的收益,明年只有0.25.

如果我们Generalize 这个example：

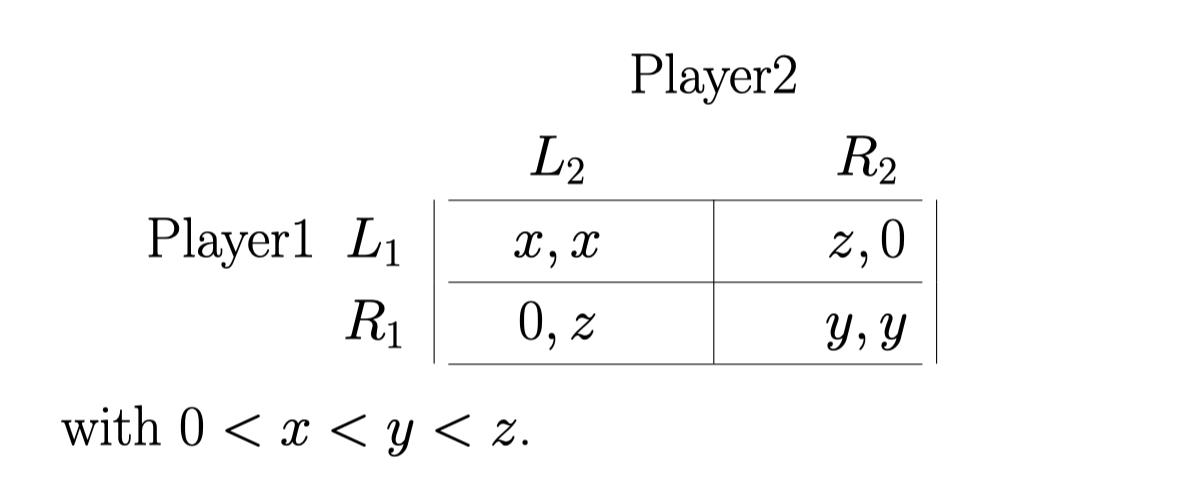
直接带入可以得出：

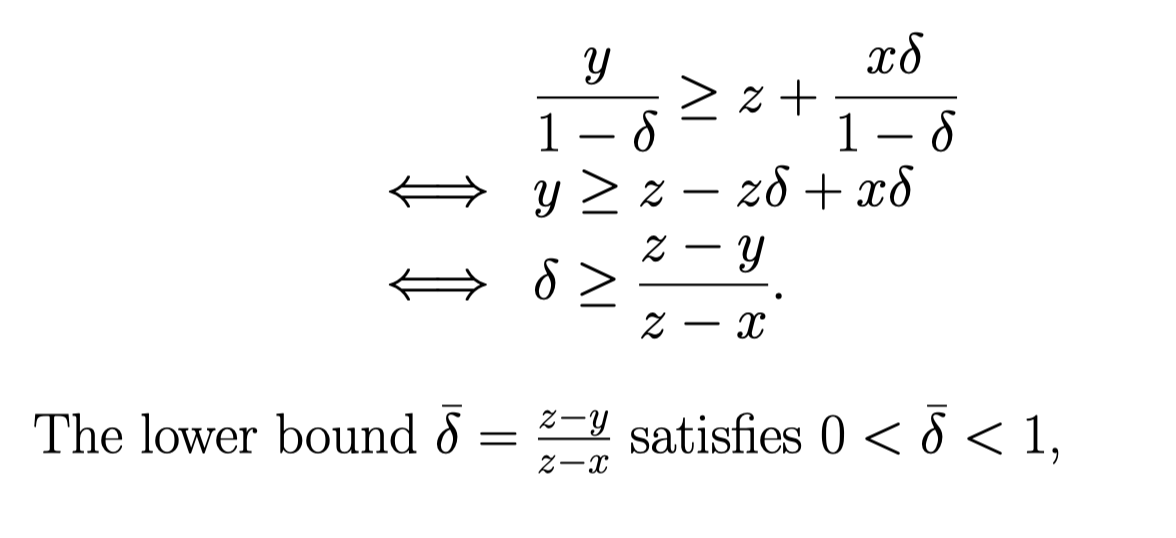
Cournot model

Notation:

\[\begin{align*} q &= \text{ quantity} \\ c &= \text{ cost of per unit} \\ p &= \text{ selling price} \\ \pi &= q(p - c) - c_0\text{ net profit (simply ignore )} c_0 \\ Q &= q_1 + q_2 \text{ the aggregate quantity of the product} \\ P(Q) &= \begin{cases} a - Q & \text{ if } Q < a \\ 0 & \text{otherwise} \end{cases}\\ & \text{ the price determined by the total quantity} \\ \pi_i(q_i, q_j) &= P(q_i + q_j) \cdot q_i - c \cdot q_i \text{} \\ &= \begin{cases} q_i[a - (q_i+ q_j) - c] & \text{ if } q_i + q_j < a \\ -cq_i & \text{ if } q_i + q_j \ge a\\ \end{cases} \\ \end{align*}\]

所以很简单的, payoff function 是一个二次函数; 最值在：

\[\begin{align*} & \max_{0 \le q_i \le a - q_j^*} q_i[a - c - q_j^* - q_i] \\ & \to \bar{q_i} = {\frac{1}{2}}(a - q_j^* - c) \text{ 对称轴 -b/2a}\\ \end{align*}\]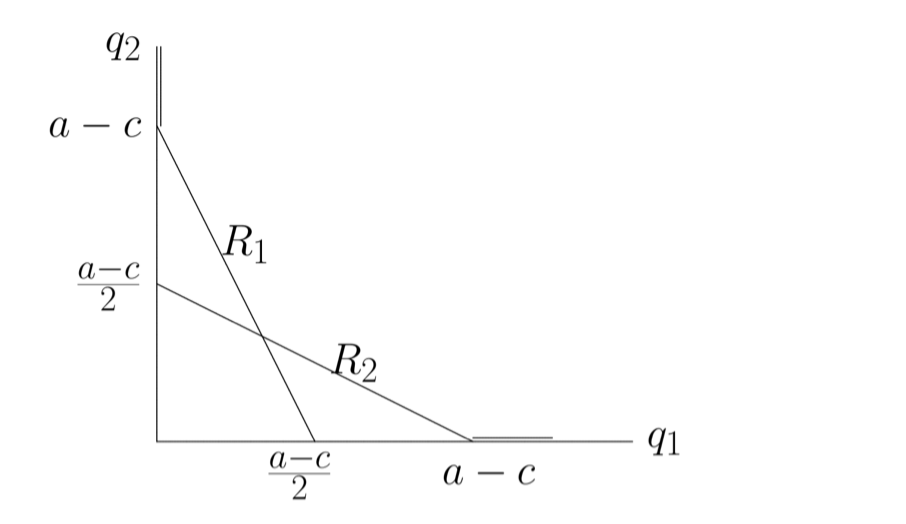

Solved: \(\begin{align*} \begin{cases} q_1^* &= {\frac{1}{3}} (a-c) \\ q_2^* &= {\frac{1}{3}} (a-c) \\ \pi_1 &= {\frac{(a-c)^2}{9}} \\ \end{cases} \\ \end{align*}\)

Collusion between Cournot Duopolists

If the two firms cooperate, then they can maximize their total profit: \(\boldsymbol{q}_{}^{}\)

\[\begin{align*} & \max \boldsymbol{q}(a - \boldsymbol{q} -c) \\ & \boldsymbol{q_m} = {\frac{a-c}{2}} \\ & q_1 = {\frac{\boldsymbol{q_m}}{2}} \\ & \pi_m = {\frac{(a-c)^2}{4}} \\ & \pi_1 = {\frac{(a-c)^2}{8}} \\ & \pi_{old} = {\frac{(a-c)^2}{9}} \\ \end{align*}\]

However, then if \( p_i = {\frac{p_m}{2}}\), the other firm cheat,

\[\begin{align*} q_1 &= {\frac{q_m}{2}} = {\frac{a-c}{4}} \\ \max q_2(a - q_2 - q_1 - c) \to q_2 &= {\frac{a -q_1 - c}{2}} \\ &= {\frac{3(a-c)}{8}}\\ \pi_d &= {\frac{9(a-c)^2}{64}} > {\frac{(a-c)^2}{8}} \\ \pi_c &= {\frac{3(a-c)^2}{32}} \\ \end{align*}\]

现在对比两个, 一直合作 vs 中途不合作

一直合作： \(\begin{align*} &{\frac{(a-c)^2}{8}} (1 + \delta + \delta^2 + \cdots)\\ & = {\frac{(a-c)^2}{8}} {\frac{1}{1- \delta}} \\ \end{align*}\) 中途不合作： \(\begin{align*} & {\frac{9(a-c)^2}{64}} + {\frac{(a-c)^2}{9}} ( \delta + \delta^2 + \cdots)\\ &= {\frac{9(a-c)^2}{64}} + {\frac{(a-c)^2}{9}} {\frac{ \delta}{1 - \delta}} \\ \end{align*}\)

Solved: \(\text{合作} \ge \text{中途不合作}\\ \delta \ge {\frac{9}{17}}\)

Chapter 3 不完全信息 静态博弈

自己有别人不知道的信息： 自己的 type

不是动态的, 所以是 Action Space 不是, Strategy Space

Notation

\[\begin{align*} n &= \text{ n players }\\ A_1, ..., A_n &= \text{ action spaces} \\ T_1, ..., T_n &= \text{ type spaces} \\ P_1, ..., P_n &= \text{ their beliefs} \\ u_1, ..., u_n &= \text{ their payoff functions}\\ & \\ G &= \{ A_1, ..., A_n ; T_1, ..., T_n; P_1, ..., P_n; u_1, ..., u_n \}\\ \end{align*}\]

Type, for player \(i, \,\, t_i \in T_i\)

只有player \(i_{}^{}\) 才知道自己是什么type.

\[u_i (a_1,..., a_n ; t_i) \text{ 不同的type 会有不同的 payoff function}\]

但别人知道你的payoff function, 只是不知道你是什么type。

Belief

对别人的猜测 (公共的信息,) 别人也知道你是怎么猜的

\[\text{ For player } i \\ P_i (t_{-i} | t_i) \text{ 当自己是type ti 的时候, 对别人所有的 type 的分布概率的预计}\]

Stategy

就是每一个 type, 应该对应一个action, 就像Cournot 一样, \(c_H , c_L\) 有两个action。

Bayesian Nash equilibrium

for strategies \(s^* = (s^*_1, ..., s^*_n)\) are a pure-strategy Bayesian Nash equilibrium if:

For each player \(i_{}^{}\) , for each type \(t_{i}^{} in T_i\) \(\begin{align*} & \\ \max_{ a_i \in A_i} &= \mathbb{E}_{t_{-i}} u_i(a_i, s^*_{-i} (t_{-i}); t_i) \\ & \text{ 每一个人的 每一个 type 的action 都让它这个 type 的payoff 最大化}\\ \end{align*}\)

Cournot Competition under asymmetric information

现在 Cournot model, 但是有一点小改变。

\[\begin{align*} c_1 (q_1) &= cq_1 \\ c_2(q_2) &= \begin{cases} c_H q_2 & \text{ with probability } \theta \\ c_L q_2 & \text{ with probability } 1- \theta \\ \end{cases} \\ \end{align*}\]

Firm 1 的成本是大家都知道的, 但是 Firm 2 的成本只有它自己知道。Firm 1 的视角里, Firm 2 的成本就是 那个概率。

然后两个firm 同时choose \(( q_1^*, q_2^* (c_H), q_2^*(c_L))\)

\[\begin{align*} q_2^*(c_H) &= \max_{q_2} [a - q_1^* - q_2 - c_H] q_2 \\ & \text{ 当firm 2 是 High cost 的时候, 选择} q_2^* \text{ 当最佳的生产数量} \\ q_2^*(c_L) &= \max_{q_2} [a - q_1^* - q_2 - c_L] q_2 \\ & \text{ 当firm 2 是 Low cost 的时候, 选择} q_2^* \text{ 当最佳的生产数量} \\ \end{align*}\]

容易得, 这是个二次函数, 所以还是根据以前的结论, 最高值在：

\[q_2^* (c_H) = {\frac{ a - q_1^* - c_H}{2}} \\ q_2^* (c_L) = {\frac{ a - q_1^* - c_L}{2}} \\\]

从 Firm 1 的视角, 它的 payoff function 是这样的：

\[\begin{align*} \pi_1( q_1) &= \theta \boxed{[a - q_1 - q_2^*(c_H) - c]q_1} + (1- \theta) \boxed{[ a - q_q - q_2^* (c_L) - c] q_1} \\ &= [(a - \theta q_2^* (c_H) - (1 - \theta) q_2^* (c_L) - c) - q_1]q_1\\ \end{align*}\]

这也是一个二次函数:

\[\begin{align*} q_1^* &= {\frac{[a- \theta q_2^* (c_H) - (1 - \theta) q_2^* (c_L) - c]}{2}} \\ &= {\frac{[a - \theta {\frac{ a - q_1^* - c_H}{2}} - (1 - \theta) {\frac{ a - q_1^* - c_L}{2}} - c]}{2}} \\ &= {\frac{[ {\frac{a}{2}} + {\frac{q_1^*}{2}} - \theta {\frac{- c_H}{2}} - (1 - \theta) {\frac{ - c_L}{2}} - c]}{2}} \\ &= {\frac{[ {\frac{a}{2}} + {\frac{q_1^*}{2}} + \theta {\frac{c_H}{2}} + (1 - \theta) {\frac{ c_L}{2}} - c]}{2}} \\ & \Updownarrow \\ 4q_1^* &= a + q_1^* + [ \theta c_H + (1 - \theta) c_L] - 2c \\ 3q_1^* &= a + [ \theta c_H + (1 - \theta) c_L] - 2c \\ \end{align*}\]

Then it solve:

\[\begin{align*} q_2^* (c_H) &= {\frac{ a - q_1^* - c_H}{2}} \\ &= {\frac{1}{6}}( a - 2c + [ \theta c_H + (1 - \theta) c_L]) + {\frac{a - c_H}{2}} \\ & \\ q_2^* (c_L) &= {\frac{ a - q_1^* - c_L}{2}} \\ &= {\frac{1}{6}}( a - 2c + [ \theta c_H + (1 - \theta) c_L]) + {\frac{a - c_L}{2}} \\ \end{align*}\]

Public Good example 公共资源

现在有两个 player i = 1,2, 它们只能选 贡献 或 不贡献。两个人只要有一个人贡献, 就有 1 的回报, 但是如果贡献, 得损失 一定的利益。 如果两个人都不贡献, 那两个人的回报都是 0.

player i 的 type 是 \(c_i\), 这个type 的贡献的利益就是 \( c_1\)

现在 假定 player 1 有两个type , \(c_1 = 0.5\) or \(c_1 = 1.2\). 外界(正确的)认为它的两个type的概率各是 0.5。

Player 2 只有一个 type , c_2 = 0.8.

所以 我们可以先把两个 payoff table 画出来

C: Contribute D: 不贡献

所以, 对player 1 来说

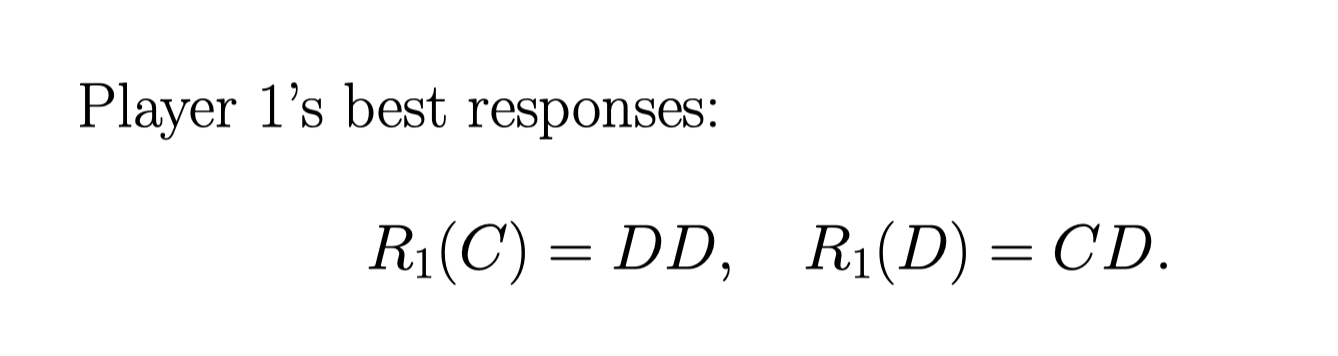
对 player 2 来说, 它只有一种 payoff table：

Player 2 的 \(c_2\) 是0.8, 所以 如果如果它 贡献的话 收益说 0.2, 不贡献的话, 可能是0 也可能是1

比如, Player 1 出 C, 如果 player 1 出 CC, 那就是说, \(u_2(CC,C) = P(c1 = 0.5) \times 0.2 + P(c_1 = 1.2) \times 0.2 = 0.2\)

同理我们可以得到这个表：

然后我们得结合这两个表, 去找到它们相交的地方。 所以 (DD, C) (CD, D) 是两个 纳什均衡。

如果 player 2 也有两个 type

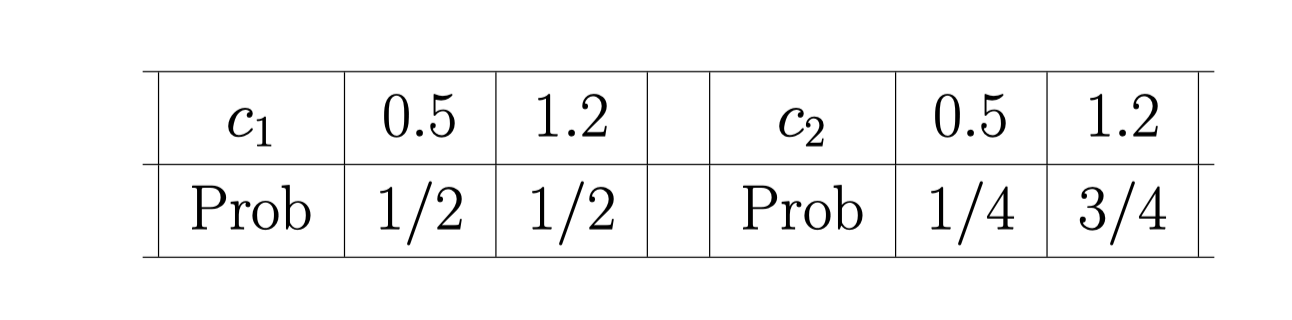
这样的话, 我们还是先考虑 player 1. 它的 expected payoff (根据 player 2) 是

这个例子特殊, 当自己是 \(c_1 = 0.5\) 的时候, player 2 不管是哪个, player 1 的payoff 都是一样的。

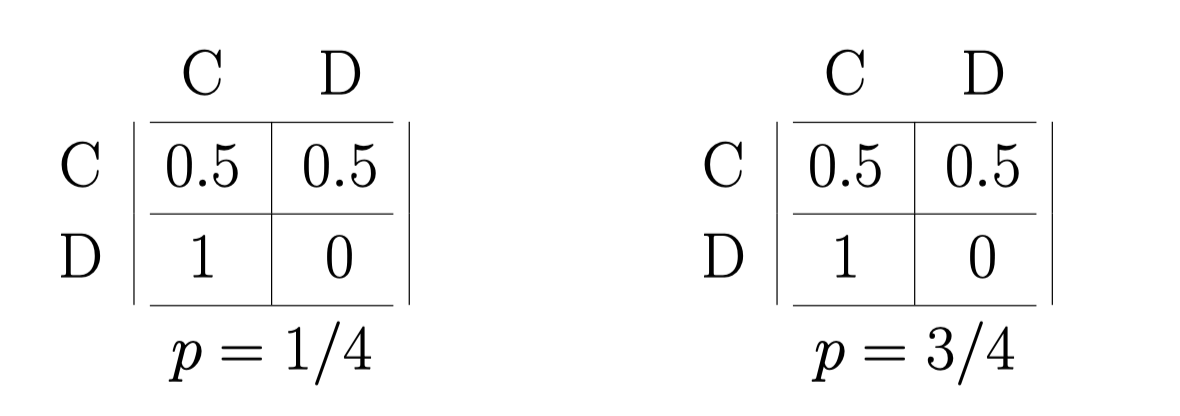
但是注意, 现在player 2 有两个情况, 所以它可以选两次。

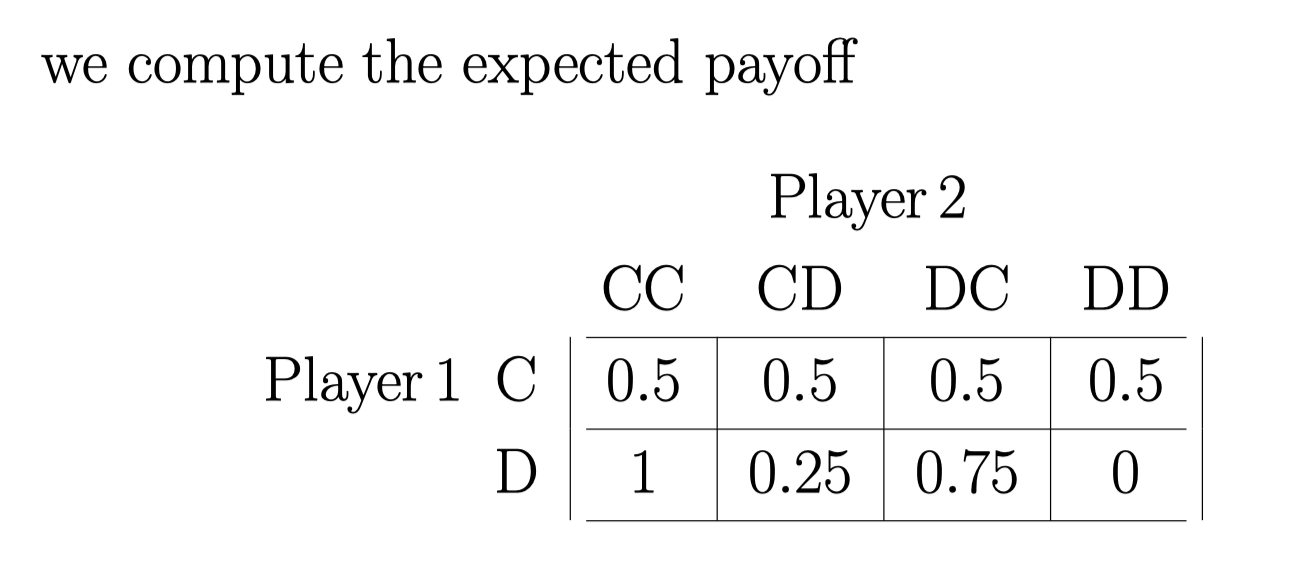
比如说 \(u_1 (C, CD ;c_1 = 0.5) = {\frac{1}{4}} \times 0.5 + {\frac{3}{4}} \times 0.5 = 0.5\)

\[u_1 (D, CD; c_1 = 0.5) = {\frac{1}{4}} \times 1 + {\frac{3}{4}} \times 0 = 0.25\]

所以我们得先得到这个表：

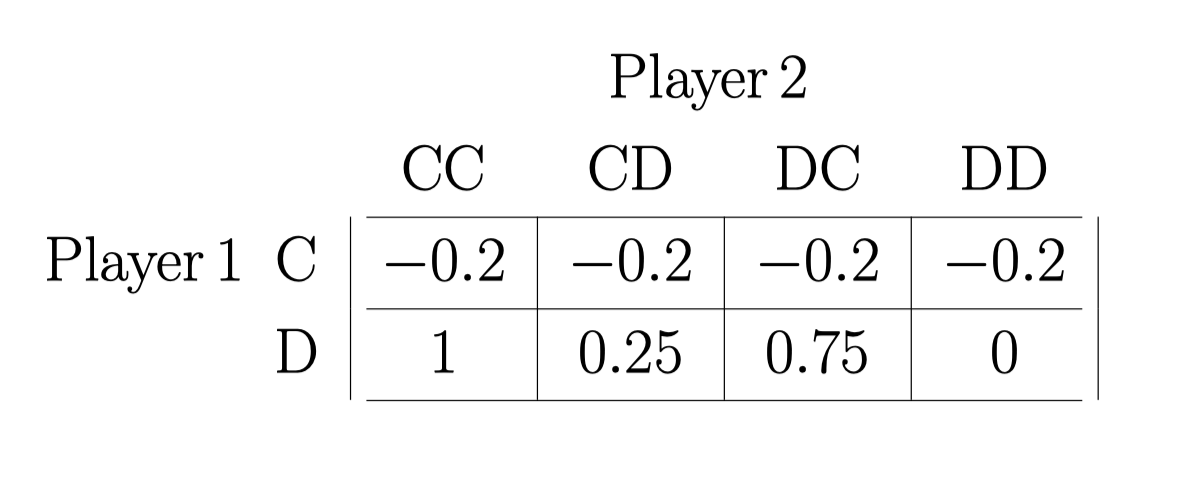
然后 如果 player 1 的 type 是 \(c_1 = 1.2\) : 同理也要的这个表

至此, 我们能得到 Best responses

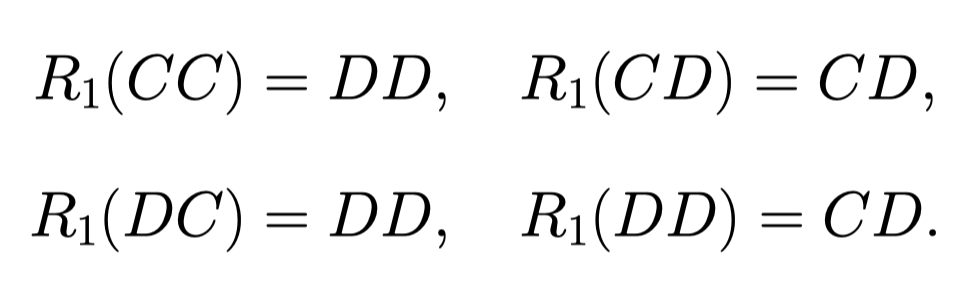
同理, 我们再把 Player 2 的情况弄清楚：

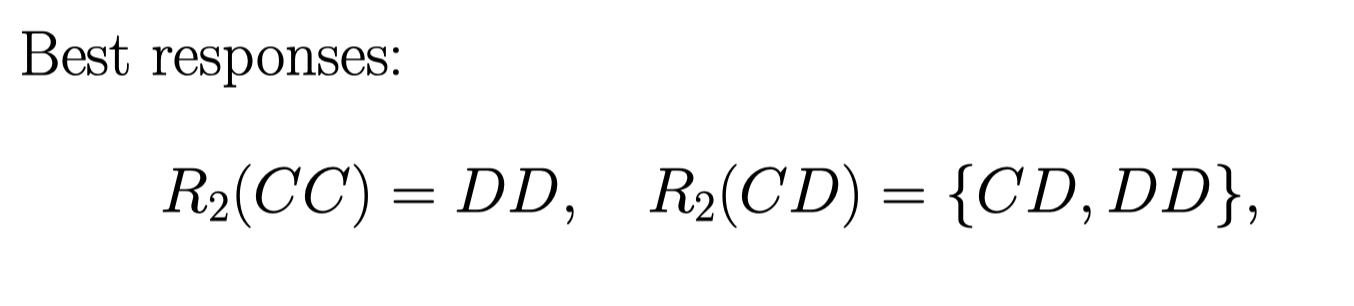
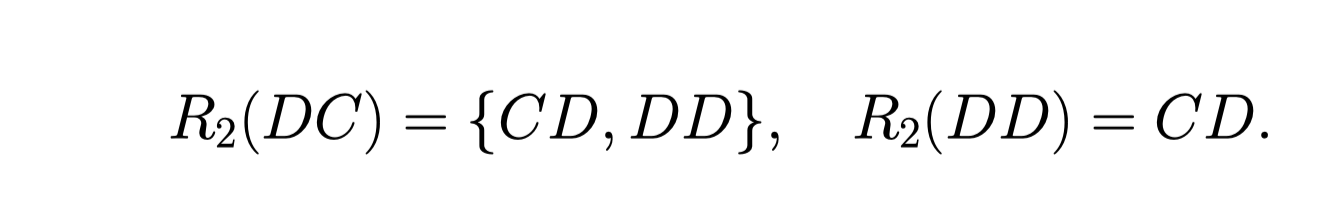
最后我们得到,

Chapter 4 不完全信息 动态博弈

Perfect Bayesian Equilibrium

首先来一个例子。

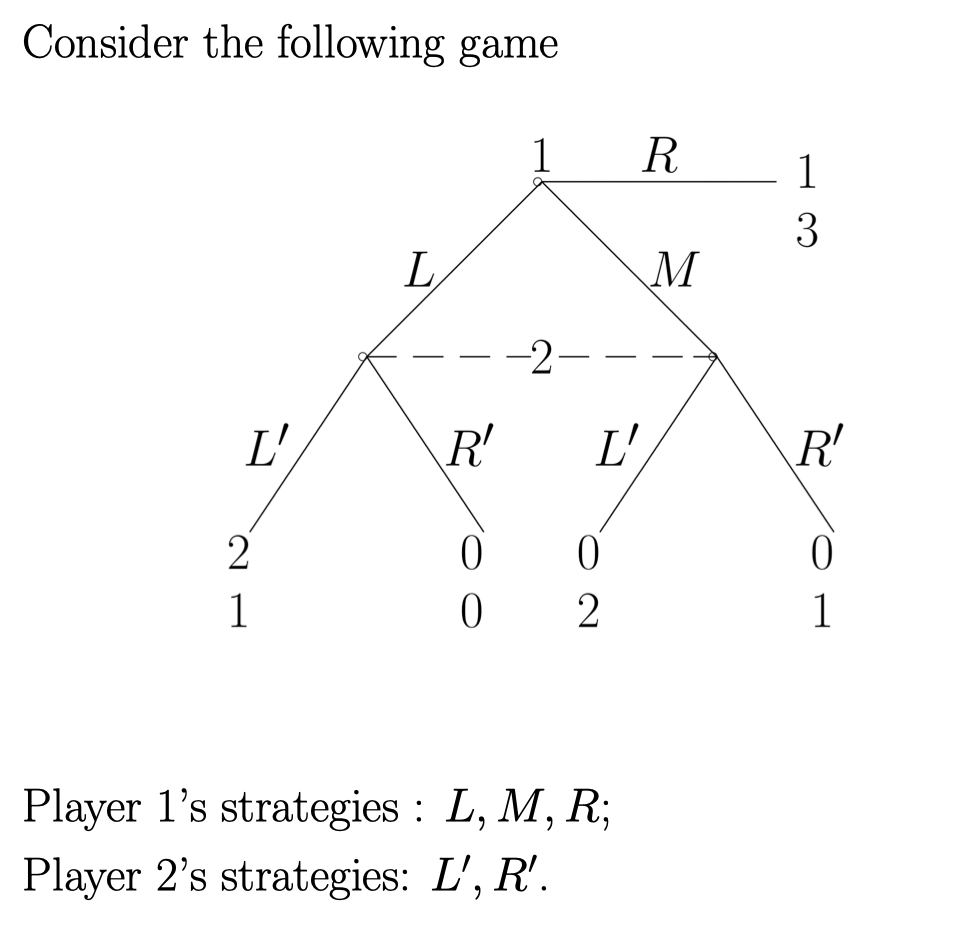
我们如果用 Best Response 这个最general 的方法：

会得到两个 Nash equilibria. 但是第二个是一个 Noncredible Threat 现在的问题是我们怎么去去除这个 NE。 (Note 这个game 没有 subgame 以前我们可以用 subgame perfect 来判断)

有一个方法是, 因为主要的问题是 player2 不知道 player 1 玩的 L 还是 M。 所以不好计算。 所以我们给它一个believe, player 2 判断 player 1 有多大机率玩的 L 或 M。

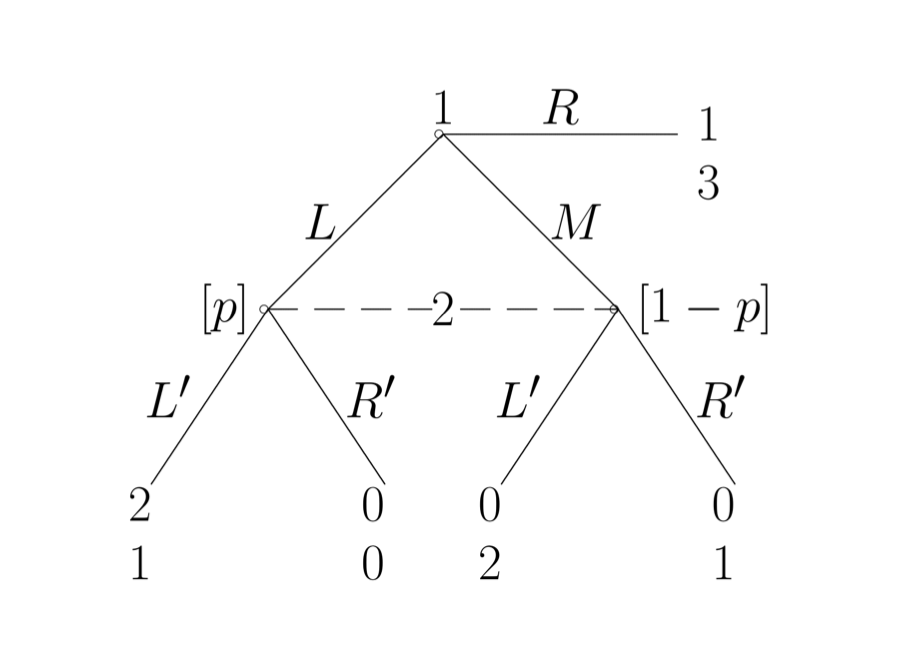
这样player 2 的 期望payoff 就是：

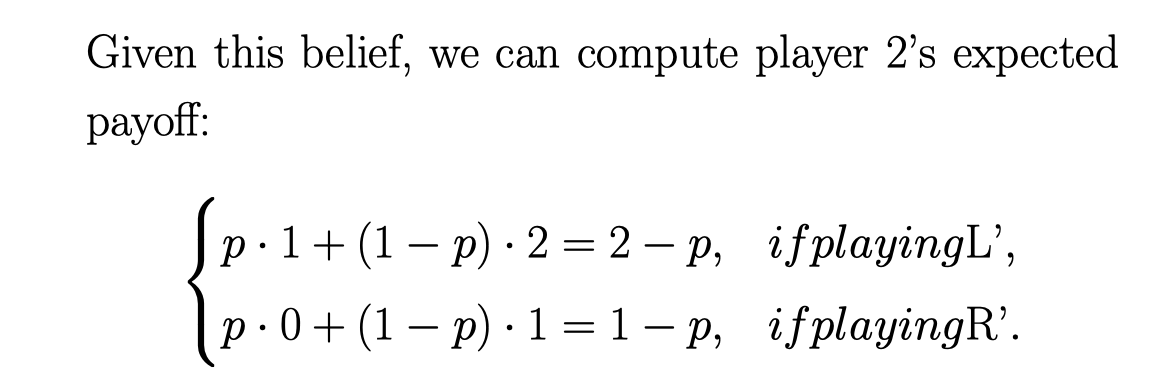
所以 2 - p > 1 - p , 我们就可以把 R’ 去掉了

但是有时候, 不同的believe 可能会有不同的选择。

比如这个例子：

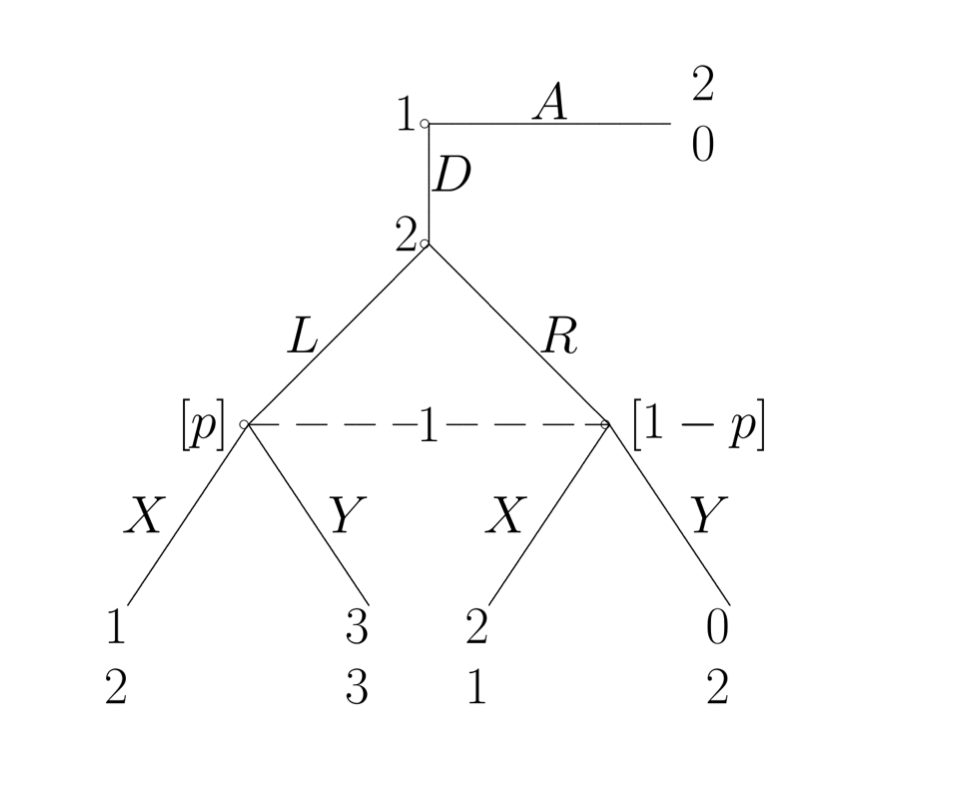
如果 player 1 认为 p = 0, 那 player 2 一定会出 R, 自己就会出 X。 但是如果 player 1出 X, player 2 其实应该出 L。 所以 这样就会让player 1 的收益 为1, 那样还不如一开始选 A。 所以(AX, L) 是一个solution。

但是如果我们看 NE：

最后的 NE是：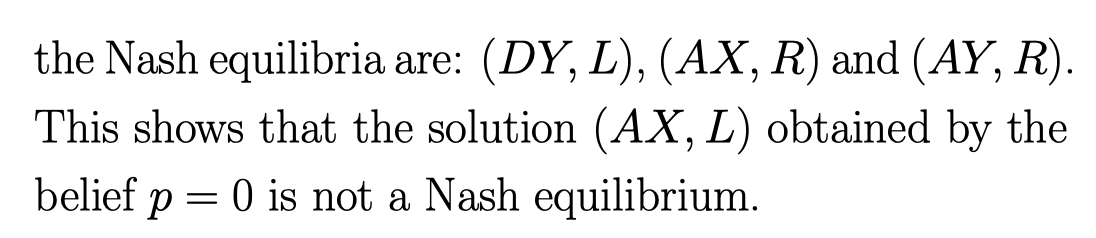

所以, p = 0, 不是一个 NE。

如何限制 believe

Perfect Bayesian equilibrium

Definition: Perfect Bayesian equilibrim 的 strategies 和 beliefs 要满足下面两个条件。

sequentially rational

就是belief 要 让 action optimal

consistency

每个 beliefs are determined by Bayes’ rule and the players’ strategies.

注意： 这个 belief 是大家都知道的。

Example 1 举个例子：

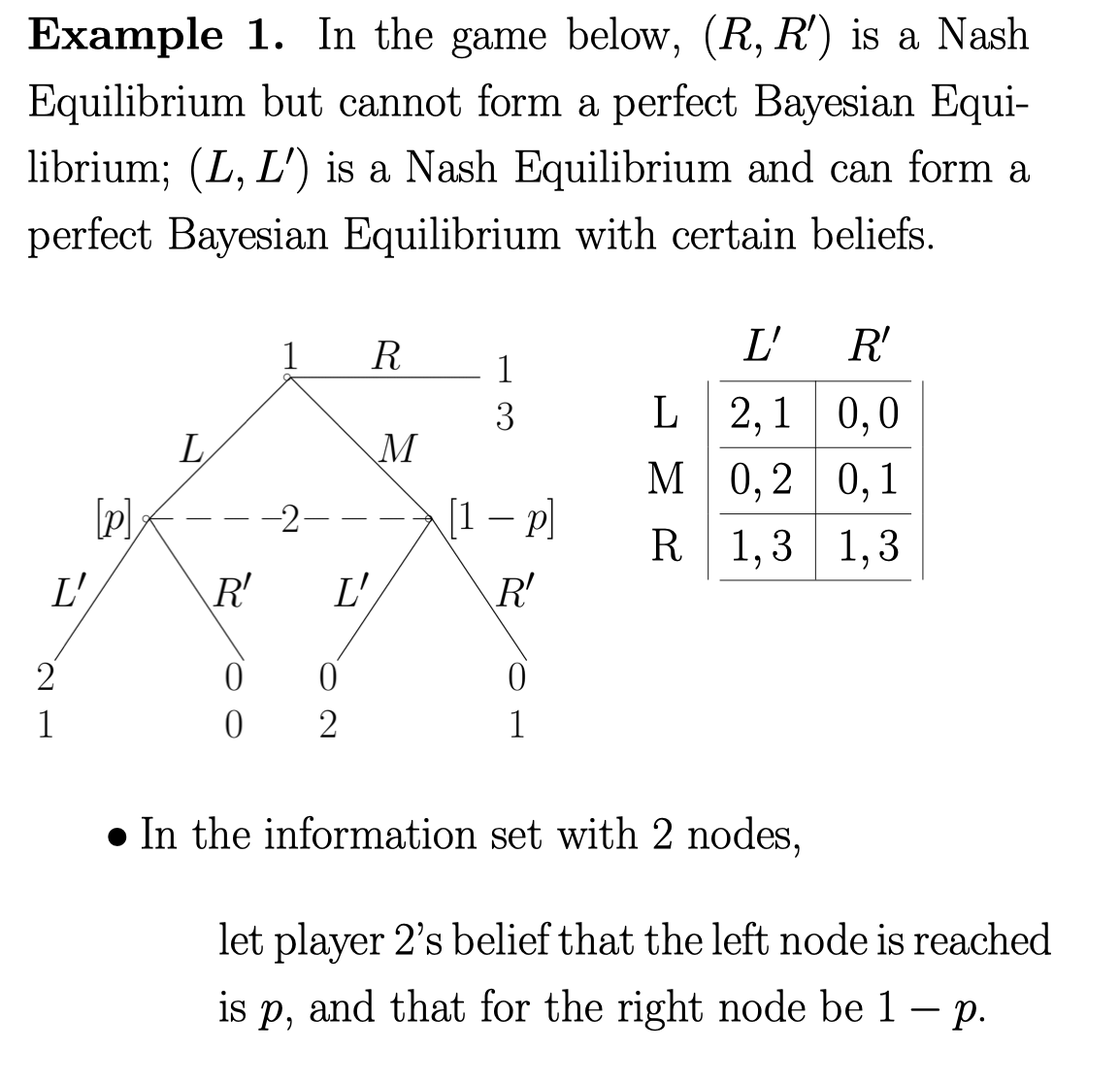
这个例子的 \( (R, R’) \) 是一个 RE, 但不是一个 Perfect Bayesian Equilibrium \( (L, L’) \) 是一个 RE, 可以是一个 Perfect Bayesian Equilibrium 在适当的believe的时候。

解释：

(R, R’)

• Consistency, 如果player 1 选 R, 根本达不到 stage 2, 所以 p 可以是任意值
• Sequential rationality, 把 p 代入发现 L’ expected payoff is 2 - p. R’ 的 expected payoff 是 1 - p . 所以 R’ 根本不是 optimal 所以不是一个 P B E。

(L, L’)

• Consistency. 既然player 1 选 L, 那 P = 1
• Sequential rationality. 如果 P = 1 , 带进去发现 L’ 确实是一个 optimal。 然后我们还要对player 1 判定。 (有点像 倒过来求的那个) Player 1 的 payoff L = 2, M= 0, R= 1 所以对player 1 也是 optimal,

综上, (L, L’) 确实是一个 optimal

Example 2

Signaling Games

Notation

有两个角色的人, 一个是 Sender (S) 一个是 Receiver (R)。

现况的 space 是 \(T = \{t_1,t_2,...,t_I\}\)

有一个概率分布 \(P(t_i)\)

S 可以提前观察到现况, 然后发消息m 给 R。

\[m \in M = \{ m_1, .., m_J \}\]

R 根据 消息 m 作出 action \(a \in A = \{ a_1, ..., a_K \}\).

Payoff: \(U_s(t_i, m_j, a_k)\) \(U_R(t_i,m_j,a_k)\)

一个最简单的两个 message type 两个 state t 的例子：

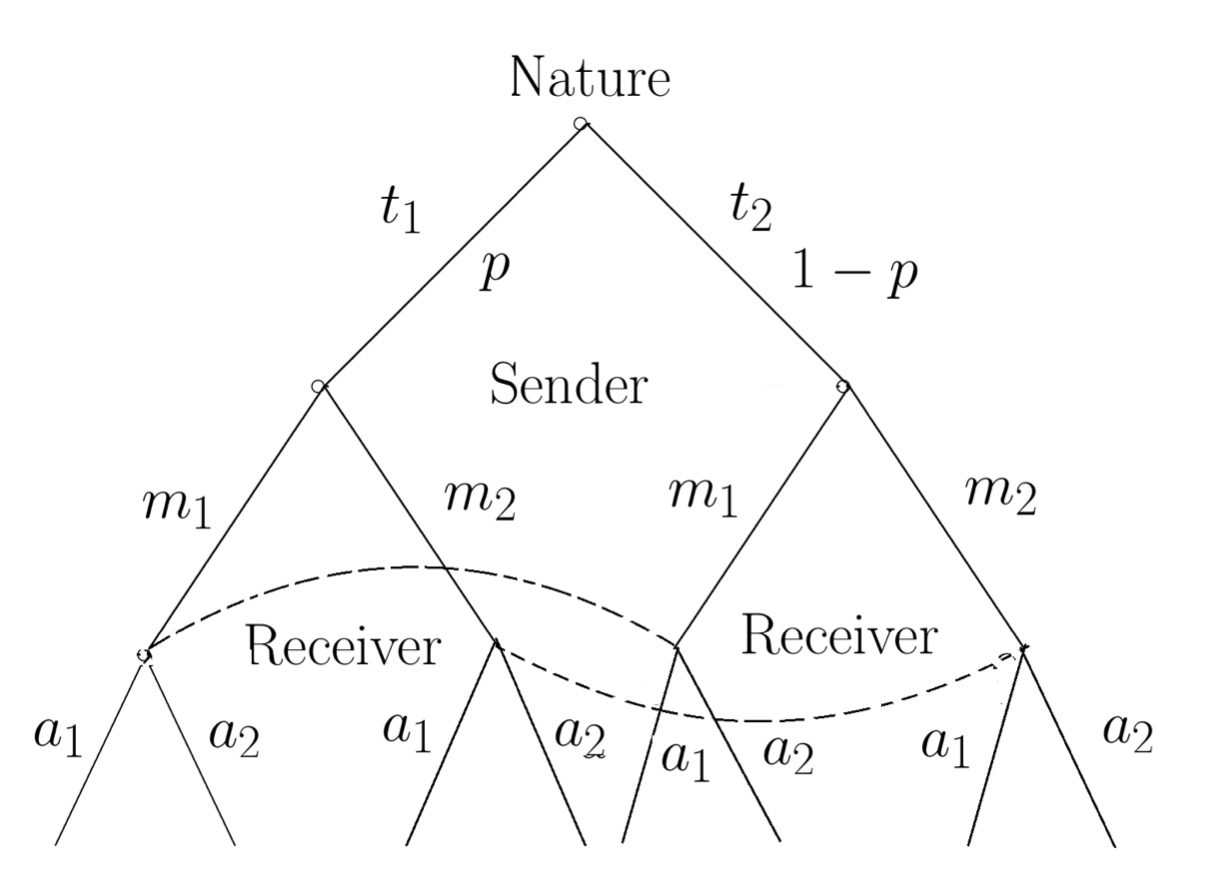
或者是

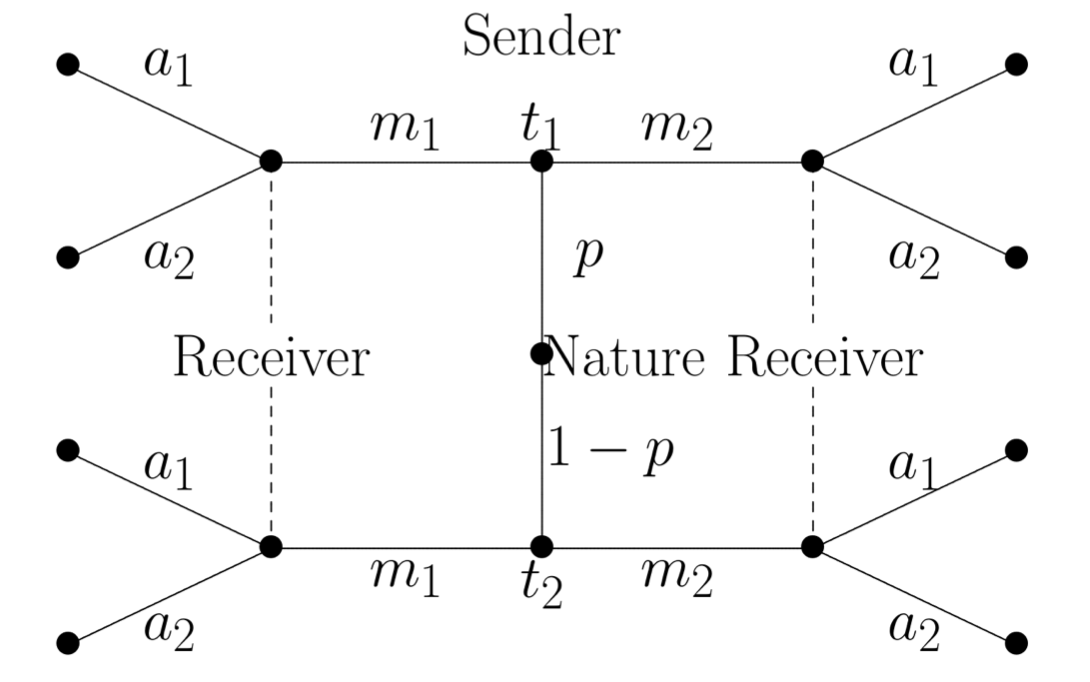
Chapter 5 合作博弈

Payoff pairs

Notation:

\[\begin{align*} H &\subset R^2 \text{ is the payoff pair} \\ d &= (d_1, d_2) \in H \text{ the point d is called the threat point} \\ u &\in H \text{ iff a joint action of two players to achieve the payoff u. } \\ \Gamma &= (H,d) \text{ two person bargaininng game}\\ W &= \text{ set of two person bargaining games} \\ \end{align*}\]

Definition:

1. Dominates :

\[(u,v) \text{ dominates } (u^\prime, v^\prime) \text{ if } u \ge u^\prime \,\, and \,\, v \ge v^\prime\]

1. Pareto optimal

If a payoff pairs are not dominated by any other pair : Pareto optimal

1. Two person bargaining game - \(W_{}^{}\)

• if \(H \subset \mathbb{R}^{2}\) is compact and convex
• \(d \in H\) and
• \(H_{}^{}\) contains at least one element, such that u » d.

1. Nash bargaining solution is a mapping \(f: W \to \mathbb{R}^{2}\)

Example

Labour- management

企业家 action space \(L_{}^{}\) 要多少Labor 和工会组织 \(w_{}^{}\) 工资 ：

工会的payoff (utility)： \(u(L, w) = \sqrt{ L w}\)

企业的payoff (utility) \(\pi = L(100 - L) - wL\)

所以 $$ H = { (u,\pi) \vert u = \sqrt{L w}, \pi = L (100 -L) - wL }

(0,0) is the threat point

The Nash bargaininng solution maximizes the function

\[(u - d_1) (\pi - d_2) = \sqrt{L w} [ L(100 - L) - wL]\]

Definition n-person Cooperative Games

\[\begin{align*} N &= \{ 1,2,...,n \} \\ S &\subseteq N \text{ coalition, nonempmty sebset of N} \\ v(S) &= \text{ characteristic function for coalition } S\\ \Gamma &= (N, v) \text{ the game} v( \emptyset) = 0 \\ v(K \cup L) \ge v(K) + v(L) \end{align*}\]

Example

The drug game & the Garbage game